
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Ньютона. Если f(x) имеет непрерывную производную и − дважды непрерывно дифференцируемая функция, тогда
|
|
Если f(x) имеет непрерывную производную и 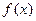 − дважды непрерывно дифференцируемая функция, тогда, выбрав в (2.3)
− дважды непрерывно дифференцируемая функция, тогда, выбрав в (2.3) 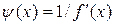 , получаем эквивалентное уравнение
, получаем эквивалентное уравнение 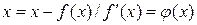 . Т.е. рекуррентная последовательность метода Ньютона
. Т.е. рекуррентная последовательность метода Ньютона
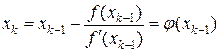 (1.6)
(1.6)
 Из (1.6) видно, что этот метод одношаговый (m=1) и для начала вычислений требуется задать одно начальное приближение x0 из области сходимости
Из (1.6) видно, что этот метод одношаговый (m=1) и для начала вычислений требуется задать одно начальное приближение x0 из области сходимости
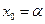 при
при 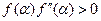
или
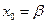 при
при 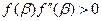 ).
).
Метод Ньютона получил также второе название метод касательных благодаря геометрической иллюстрации его сходимости, представленной на рис. 1.2. Этот метод позволяет находить как простые, так и кратные корни.
Основной его недостаток - малая область сходимости и необходимость вычисления производной f'(x). Структурная схема алгоритма отличается от предыдущей только формулой вычисления x1 через x0.