
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перед выполнением данной работы необходимо изучить содержимое пункта “ Концепция модульного программирования ”.
|
|
Лабораторная работа №5 -А Использование подпрограмм
1. Даны действительные числа 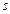 ,
, 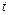 . Получить
. Получить
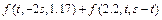 ,
,
где
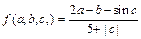 .
.
2. Даны действительные числа 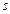 ,
, 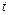 . Получить
. Получить
 ,
,
где
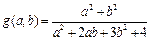
- Даны действительные числа
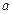 ,
, 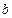 ,
, 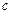 . Получить
. Получить
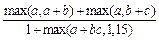 .
.
- Даны действительные числа
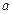 ,
, 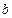 . Получить
. Получить
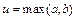 ,
, 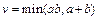 ,
, 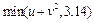 .
.
5. Даны действительные числа 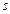 ,
, 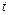 . Получить
. Получить
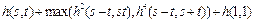 ,
,
где
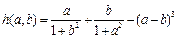 .
.
- Даны действительные числа
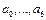 . Получить значение
. Получить значение 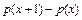 , где
, где
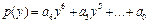 .
.
- Даны действительные числа
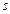 ,
, 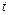 ,
, 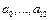 . Получить
. Получить 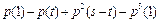 , где
, где
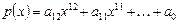 .
.
- Даны действительные числа
 ,
, 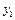 ,
, 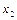 ,
, 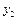 , …,
, …, 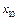 ,
, 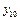 . Найти периметр десятиугольника, вершины которого соответственно координаты
. Найти периметр десятиугольника, вершины которого соответственно координаты 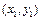 ,
, 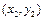 , …,
, …, 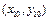 . Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами.
. Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами. - Дано натуральное число
 , действительные числа
, действительные числа  ,
, 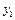 ,
, 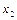 ,
, 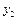 , …,
, …, 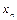 ,
, 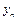 . Найти площадь
. Найти площадь  -угольника, вершины которого при некотором последовательном обходе имеют координаты
-угольника, вершины которого при некотором последовательном обходе имеют координаты 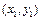 ,
, 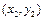 , …,
, …,  . Определить процедуру вычисления площади треугольника по координатам его вершин.
. Определить процедуру вычисления площади треугольника по координатам его вершин. - Дано четное число
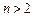 ; проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнута и полностью не доказана) заключается в том, что каждое четное число
; проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнута и полностью не доказана) заключается в том, что каждое четное число  , большее двух, представляется в виде суммы двух простых чисел. Определить процедуру, позволяющую распознавать простые числа.
, большее двух, представляется в виде суммы двух простых чисел. Определить процедуру, позволяющую распознавать простые числа. - Дано натуральное число
 . Выяснить, имеются ли среди чисел
. Выяснить, имеются ли среди чисел  ,
, 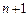 , …,
, …, 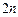 близнецы, т.е. простые числа, разность между которыми равна двум. Определить процедуру, позволяющую распознавать простые числа.
близнецы, т.е. простые числа, разность между которыми равна двум. Определить процедуру, позволяющую распознавать простые числа. - Дано натуральное число
 . Среди чисел 1, 2, …,
. Среди чисел 1, 2, …,  найти все те, которые можно представить в виде суммы квадратов двух натуральных числе. Определить процедуру, позволяющую распознавать полные квадраты.
найти все те, которые можно представить в виде суммы квадратов двух натуральных числе. Определить процедуру, позволяющую распознавать полные квадраты. - Даны натуральные числа
 ,
, 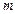 ; найти НОД (n, m). Используя программу, включающую рекурсивную процедуру вычисления НОД, основанную на соотношении НОД (n, m) = НОД (m, r), где
; найти НОД (n, m). Используя программу, включающую рекурсивную процедуру вычисления НОД, основанную на соотношении НОД (n, m) = НОД (m, r), где 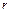 – остаток от деления
– остаток от деления  на
на 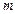 .
. - Даны натуральные числа
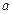 ,
, 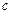 ,
, 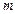 . Получить
. Получить 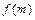 , где
, где
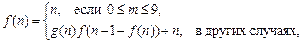
где 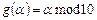 .
.
Использовать программу, включающую рекурсивную процедуру вычисления  .
.
- Даны неотрицательные целые числа
 ,
, 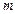 ; вычислить
; вычислить 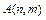 , где
, где
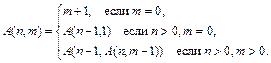
Это функция Аккермана. Использовать программу, включающую рекурсивную процедуру.
- Два натуральных числа называются «дружественными», если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284). Напечатать все пары “дружественных” чисел, не превосходящих заданного натурального числа.
- Даны координаты вершин двух треугольников. Определить, какой из них имеет большую площадь.
- Даны координаты вершин треугольника и координаты некоторой точки внутри него. Найти расстояние от данной точки до ближайшей стороны треугольника. При определении расстояний учесть, что площадь треугольника может вычисляться разными способами - через три его стороны или через основание и высоту.
- Три прямые на плоскости заданы уравнениями
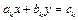
(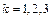 ). Если эти прямые попарно пересекаются и образуют треугольник, найти его площадь.
). Если эти прямые попарно пересекаются и образуют треугольник, найти его площадь.
- Даны коэффициенты многочленов
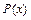 и
и 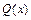 15-й степени и дано вещественное число
15-й степени и дано вещественное число 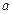 . Вычислить величину
. Вычислить величину 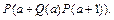
- Составить программу вычисления площади кольца по значениям внутреннего и внешнего радиусов, используя подпрограмму вычисления площади круга (2 варианта: с процедурой и с функцией).
- Даны три целых числа. Определить, сумма цифр которого из них больше. Подсчет суммы цифр организовать через подпрограмму.
- На плоскости заданы своими координатами п точек. Составить программу, определяющую, между какими из пар точек самое большое расстояние. Указание. Координаты точек занести в массив.
- Составить программу, которая в массиве A [ N ] находит второе по величине число (вывести на печать число, которое меньше максимального элемента массива, но больше всех других элементов).
- Составить программу, проверяющую, являются ли данные три числа взаимно простыми.
- Даны две дроби
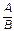 и
и 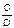 (А, В, С, D — натуральные числа). Составить программу для деления дроби на дробь, для умножения дроби на дробь, для сложения этих дробей, для вычитания из первой дроби второй. Результат должен быть несократимой дробью.
(А, В, С, D — натуральные числа). Составить программу для деления дроби на дробь, для умножения дроби на дробь, для сложения этих дробей, для вычитания из первой дроби второй. Результат должен быть несократимой дробью. - Составить программу для вычисления суммы факториалов всех четных чисел от m до n.
- Найти все простые натуральные числа, не превосходящие n, двоичная запись которых представляет собой палиндром, т.е. читается одинаково слева направо и справа налево.
- Имеется часть катушки с автобусными билетами. Номер билета шестизначный. Составить программу, определяющую количество счастливых билетов на катушке, если меньший номер билета — N, больший — М (билет является счастливым, если сумма первых трех его цифр равна сумме последних трех).
- Составить программу для разложения данного натурального числа на простые множители. Например,
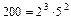 .
.