
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розрахунку на механічну міцність робочого валка стана ХПТ-75
|
|
На робочий валок (див. мал. 1) діє вертикальне зусилля прокатки, сточувальні та розрахункові зусилля відничих шестернь, а також крутильний момент.
Вихідні данні стана ХПТ-75:
Рm =1500 кН; Мпр. max =83 кН·м; Dв. =336 мм; L1 = 317, 5 мм; L2 =337, 5 мм; L 3 =202, 5 мм; L 4 =135 мм; L 5 =100 мм; d =365 мм; d1 =180 мм; d2 =205 мм; d3 =195 мм; d4 =220 мм; r =182 мм; b2 =140 мм; b3 =80 мм; h =160 мм; b =33 мм;
Розрахунок
1 Крутильний момент, діючий на одну шийку робочого валка
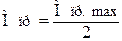 , Н (2.36)
, Н (2.36)
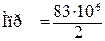 Н·мм
Н·мм
2 Оточувальне зусилля на відничій шестерні
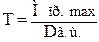 , (2.37)
, (2.37)
де Dв. ш. – діаметр початкового кола ведучої шестерні
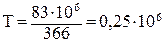 Н
Н
3 Розпіркове зусилля
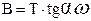 , (2.38)
, (2.38)
де 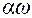 - кут прямозубого зачіплювання,
- кут прямозубого зачіплювання, 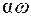 = 200
= 200
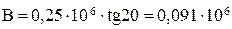 Н
Н
4 Опорні реакції у вертикальній площині
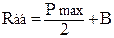 , (2.39)
, (2.39)
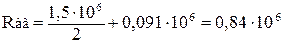 Н
Н
5 Опорні реакції у горизонтальній площині
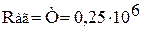 Н
Н
6 Визначаємо напруження в перерізі 1 – 1
6.1 Згинальний момент у вертикальній площині
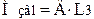 , (2.40)
, (2.40)
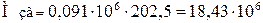 Н·мм
Н·мм
6.2 Згинальний момент у горизонтальній площині
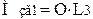 , (2.41)
, (2.41)
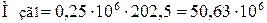 Н·мм
Н·мм
6.3 Сумарний згинальний момент
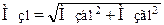 , (2.42)
, (2.42)
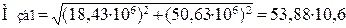 Н·мм
Н·мм
6.4 Напруження згинання
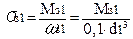 , (2.43)
, (2.43)
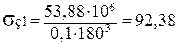 мПа
мПа
6.5 Напруження обертання
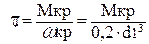 , (2.44)
, (2.44)
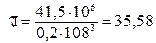 мПа
мПа
6.6 Сумарне напруження у перерізі 1 – 1
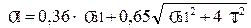 <
< 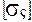 , (2.45)
, (2.45)
де 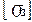 - допустиме напруження згинання для матеріалу валка,
- допустиме напруження згинання для матеріалу валка,
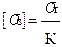 , (2.46)
, (2.46)
тут 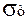 - межа текучості матеріалу валка, для сталі 30ХГСА,
- межа текучості матеріалу валка, для сталі 30ХГСА, 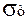 = 850 мПа
= 850 мПа
К – коефіцієнт заноса міцності, враховуючи роботу валка при великих навантаженнях приймаємо К= 2, 5
Тоді  мПа
мПа
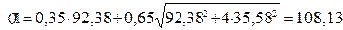 мПа
мПа
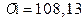 мПа <
мПа < 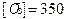 мПа
мПа
Умови міцності виконуються.
7 Визначаємо напруження у перерізі 2 – 2
7.1 Згинальний момент у вертикальній площині
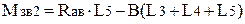 , (2.47)
, (2.47)
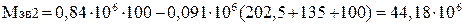 Н·мм
Н·мм
7.2 Згинальний момент у горизонтальній площині
 , (2.48)
, (2.48)
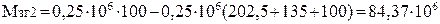 Н·мм
Н·мм
7.3 Сумарний згинальний момент
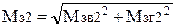 , (2.49)
, (2.49)
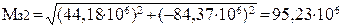 Н·мм
Н·мм
7.4 Напруження згинання
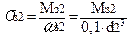 , (2.50)
, (2.50)
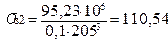 мПа
мПа
7.5 Напруження обертання
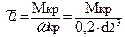 , (2.51)
, (2.51)
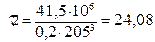 мПа
мПа
7.6 Сумарне напруження у перерізі 2 – 2
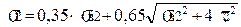 <
< 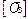 , (2.52)
, (2.52)
 мПа
мПа
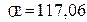 мПа <
мПа < 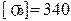 мПа
мПа
Умови міцності виконані.
8 Визначаємо напруження у перерізі 3 – 3
Переріз 3 – 3 валка (див. мал. 2) зображує собою півколо, послаблене у середині отвором центрового болта із отвором для центрового болта і з країв зевами.
8.1 Момент інерції перерізу відносно осі x – x
1 x – x = 1xx – 2·1xx – 1xx (2.53)
де 1xx – момент інерції півкруга, мм
1xx – момент інерції трикутника, мм
1xx – момент інерції прямокутника, мм
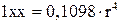 , (2.54)
, (2.54)
тут r – півкола переріза
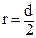 , (2.55)
, (2.55)
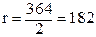 мм
мм
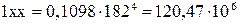 мм4
мм4
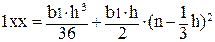 , (2.56)
, (2.56)
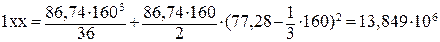 мм4
мм4
Момент інерції трикутника замінює момент інерції фігури, утворюючої зев. Цей трикутник має висоту h (див. мал. 2), та площу рівну площині фігури, утворюючої зєв. Із умови рівняння цих площин визначається основа b1 трикутника.
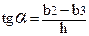 (2.57)
(2.57)
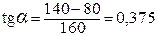 ;
; 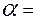 200
200
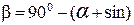 , град (2.58)
, град (2.58)
де 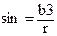 , град (2.59)
, град (2.59)
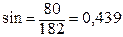 ; sin = 260
; sin = 260
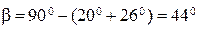
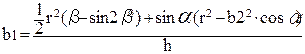 , мм (2.60)
, мм (2.60)
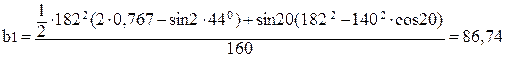 мм
мм
h - стан центра ваги перерізу
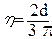 , (2.61)
, (2.61)
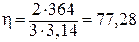 мм
мм
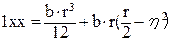 , (2.62)
, (2.62)
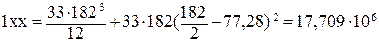 мм4
мм4
Тоді 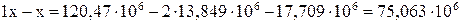 мм4
мм4
8.2 Момент інерції перерізу відносно осі у – у
1у – у = 1уу – 2·1уу – 1уу (2.63)
де 1уу – момент інерції півкола
1уу – момент інерції трикутника
1уу – момент інерції прямокутника
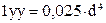 , (2.64)
, (2.64)
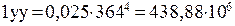 мм4
мм4
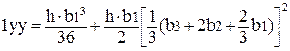 , (2.65)
, (2.65)
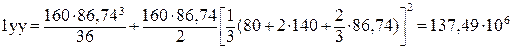 мм4
мм4
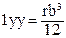 , (2.66)
, (2.66)
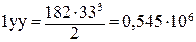 мм4
мм4
Тоді 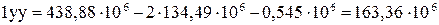 мм4
мм4
8.3 Момент опору перерізу відносно осі х – х
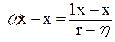 , (2.67)
, (2.67)
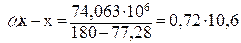 мм3
мм3
8.4 Момент опору перерізу відносно осі у – у
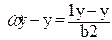 , (2.68)
, (2.68)
 мм3
мм3
8.5 Максимальне зусилля прокатки Рmax діє на валок, коли переріз 3 – 3 повернуто відносно зображеного на малюнку 2, на кут приблизно 70...800.
При розрахунку цього перерізу на максимальне зусилля прокатки приймаємо, що максимальне зусилля прокатки діє перпендикулярно осі у – у, а всебічне зусилля – перпендикулярно осі х – х
8.6 Згинальний момент у вертикальній площині
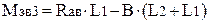 , (2.69)
, (2.69)
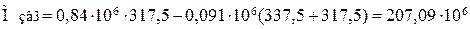 Н·мм
Н·мм
8.7 Згинальний момент у горизонтальній площині
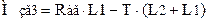 , (2.70)
, (2.70)
 Н·мм
Н·мм
8.8 Напруження згинання в перерізі 3 – 3 у моменту діючого у вертикальній площині
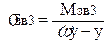 <
< 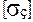 , (2.71)
, (2.71)
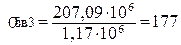 мПа
мПа
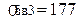 мПа <
мПа <  мПа
мПа
Умови міцності виконуються
8.9 Напруження згинання у перерізі 3 – 3 у моменту діючого у горизонтальній площині
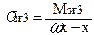 , мПа (2.72)
, мПа (2.72)
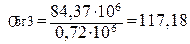 мПа
мПа
 мПа <
мПа < 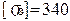 мПа
мПа
Умови міцності виконуються.
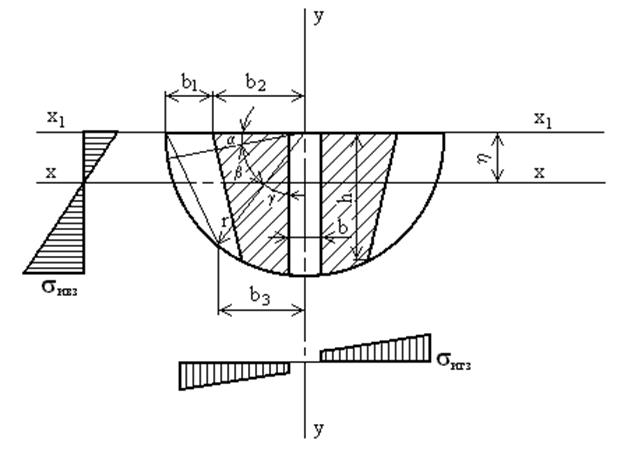
Рисунок 2.4 – Розрахункова схема перерізу 3-3 робочого валка стану ХПТ
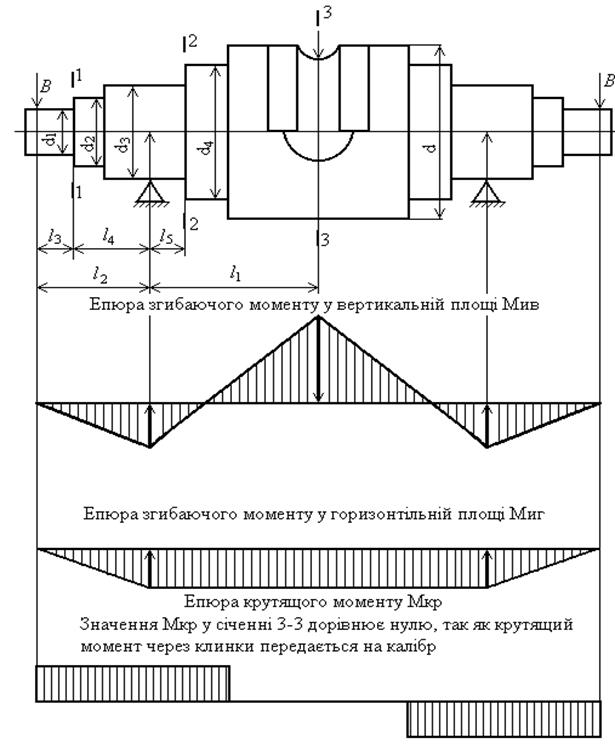
Рисунок 2.5 – Розрахункова схема робочого валка стану ХПТ