
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мета роботи. Ознайомититися з основними властивостями мереж Петрі.
|
|
Виконав
Студент групи КН-23
Житніков І. В.
Прийняв
Львів-2015
МЕТА РОБОТИ
Ознайомититися з основними властивостями мереж Петрі.
2. ТЕОРЕТИЧНІ ВІДОМОСТІ
2.1 Класифікація мереж Петрі
Автоматні мережі Петрі (state machine) − мережі у яких перехід має не більше одного входу і не більше одного виходу. Такі мережі звичайно описують послідовні процеси із розгалуженням по умові. Якщо мережа має тільки одну мітку, то мережа є, по суті, графом автомата, який послідовно переходить з одного стану в інший.
Марковані мережі (MG-мережі або market graph) − мережі, у яких кожна позиція має не більше одного входу і не більше одного виходу. За їх допомогою моделюють послідовно-паралельні процеси. MG-мережі називають також синхрографами.
Мережі вільного вибору (FC-мережі або free choice) − мережі у яких кожна дуга, що виходить з позиції, є або єдиним виходом з неї, або єдиним входом в перехід. FC-мережі використовуються для опису процесів керування..
Прості мережі − (SN-мережі або Simple nets) − мережі, у яких кожен перехід може мати не більше за одну загальну позицію з іншими переходами.
Ординарні мережі − (ON-мережі або Ordinary nets) − мережі, які не мають обмежень, окрім однієї − кратність дуг повинна бути не більше за одиницю. Між вузлами прокладається рівно один зв’язок. Неординарна мережа може бути перетворена в ординарну.
Кольорові мережі - (CPN- мережі або Coloured Petri Nets) − мережі, у яких кожна мітка має свій певний колір і перехід, пов’язаний з деякою умовою, що визначає наявність пов’язаних з ним вхідних позицій міток певного кольору. Колір мітки прийнято позначати деякою буквою.
Часові мережі Петрі − (Time Petri Nets) − мережі, у яких з кожним переходом зв’язують деяку тривалість (час). Для визначеності вважають, що вилучення фішок з вхідних позицій відбувається миттєво, а передача фішок здійснюється за встановлений час. У реальності це може відповідати роботі технічних пристроїв і підрозділів організації.
Рис.2.1. Приклад кольорової мережі Петрі
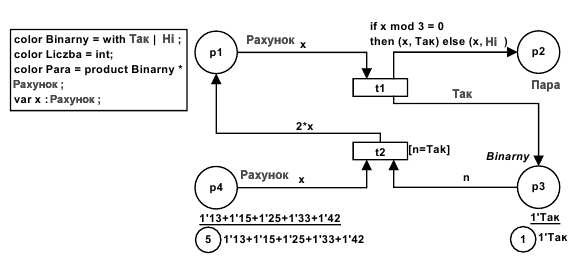
Потокові мережі − мережі, які моделюють потокові системи, в яких здійснюється управління даними. Операції виконуються одразу при готовності даних. У потоковій мережі Петрі переходи інтерпретуються як оператори або обчислювальні функції, місця інтерпретуються як черги, а дані − як фішки
2.2 Властивості мереж Петрі
Моделювання систем мережами Петрі, перш за все, зумовлене необхідністю проведення глибокого дослідження їхньої поведінки.
Аналіз складних систем на основі мереж Петрі можна виконувати за допомогою імітаційного моделювання систем масового обслуговування (СМО), представлених моделями мереж Петрі. При цьому задають вхідні потоки заявок і визначають відповідну реакцію системи. Вихідні параметри СМО розраховують шляхом обробки нагромаджених при моделюванні статистичного матеріалу.
Можливий і інший підхід до використання мереж Петрі для аналізу об'єктів, які досліджуються на системному рівні. Для проведення такого дослідження необходні методи аналізу властивостей самих мереж Петрі. Цей підхід передбачає зведення дослідження властивостей реальної системи до аналізу визначених властивостей моделюючої мережі Петрі. Він не пов'язаний з імітацією процесів і заснований на дослідженні таких властивостей мереж Петрі, як обмеженість, безпека, збереженість, досяжність, живучість.
Обмеженість.
Визначення 2.1. Позиція p P мережі Петрі PN = (P, Т, I, O) з початковим маркуванням М є k- обмеженою, якщо М’(p) k для будь-якого досяжного маркування М’ R (PN, М). Позиція називається обмеженою, якщо вона є k- обмеженою для деякого цілого значення k. Мережа Петрі обмежена, якщо всі її позиції обмежені.
Іншими словами, обмеженість – кількість міток в будь-якій позиції не може перевищувати певного значення k. При проектуванні автоматизованих систем визначення k дозволяє обґрунтовано вибирати ємкості нагромаджувачів. Можливість необмеженого зростання кількості міток свідчить про небезпеку необмеженого зростання довжин черг.
Безпечність.
Визначення 2.2. Позиція p P мережі Петрі PN = (P, Т, I, O) з початковим маркуванням М є безпечною, якщо вона є 1 - обмеженою. Мережа Петрі безпечна, якщо безпечні всі позиції мережі.
Іншими словами безпечність — частковий випадок обмеженості, зокрема це 1- обмеженість. Якщо для деякої позиції встановлено, що вона безпечна, то її можна представляти одним триґером.
Досяжність маркування.
Визначення 2.4. Для даної мережі Петрі з початковим маркуванням М і маркуванням М’ визначити, чи існує таке досяжне маркування М” R (PN, М), що М" М’.(Відношення М" М’ є істинним, якщо кожний елемент маркування М" є не меншим відповідного елемента маркування М’.)
Тобто, досяжність Mk Mj характеризується можливістю досягнення маркування Mj з стану мережі, який характеризується маркуванням Mk.
Активність.
Визначення 2.5. Активність мережі Петрі визначається можливістю спрацювання будь-якого переходу при функціонуванні об'єкту моделювання. Відсутність активності означає або надлишковысть апаратури у спроектованій системі, або свідчить про можливість виникнення зациклень, тупиків, блокувань.
Тупик в мережі Петрі — це перехід (або множина переходів), які не можуть бути запущені. У зв’язку із поняттям тупика визначимо для мережі Петрі PN із початковим маркуванням М наступні рівні активності переходів:
Рівень 0: Перехід t володіє активністю рівня 0 і називається мертвим, якщо він ніколи не може бути запущений.
Рівень 1: Перехід t володіє активністю рівня 1 і називається потенційно живим, якщо існує таке М’ R (PN, М), що t є дозволеним в М’.
Рівень 2: Перехід t володіє активністю рівня 2 і називається живим, якщо
для будь-якого М’ R (PN, М) перехід t є потенційно живим для мережі Петрі PN з початковим маркуванням М’.
Мережа Петрі називається живою, якщо всі її переходи є живими.
2.3 Граф досяжності
В основі дослідження перерахованих у п.2.2. властивостей мереж Петрі лежить аналіз досяжності.
Один з методів аналізу досяжності будь-якого маркування з стану М0 — побудова графа досяжності. Початкова вершина графа відображає М0, а решта вершин відповідають маркуванням. Дуга з Мi в Мj означає подію Mi Mj і відповідає спрацюванню перехода t.
У складних мережах граф може містити надзвичайно велику кількість вершин і дуг. Проте при побудові графа можна не відображати всі вершини, оскільки багато з них є дублями (дійсно, від маркування Mk завжди породжується один і той самий підграф не залежно від того з якого стану система прйишла в Мk). Тупики виявляються за відсутністю дозволених переходів з будь-якої вершини, тобто за присутністю листків — термінальних вершин. Необмежене зростання кількості маркерів в будь-якій позиції свідчить про порушення обмеженості.
3. ЗАВДАННЯ ДО ЛАБОРАТОРНОЇ РОБОТИ
Варіант 8


