Элементы эллиптических орбит.

Движение планеты будет определено, если известны:

- плоскость, в которой лежит её орбита,

- размеры и форма орбиты,

- ориентировка в плоскости,

- момент времени, в который планета находится в определённой точке орбиты.

Величины, определяющие орбиту планеты, называются элементами орбиты. Плоскость эклиптики является основной плоскостью, относительно которой определяется положение орбиты. 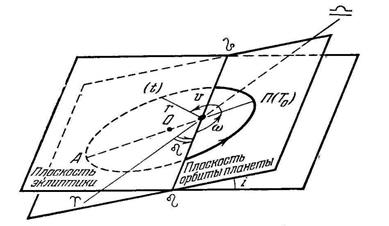Две точки, в которых орбита планеты пересекается с плоскостью эклиптики, называются узлами - восходящим и нисходящим. Восходящий узел - тот, в котором планета пересекает эклиптику, удаляясь от её южного полюса.

Эллиптическую орбиту планеты определяют 6 элементов:

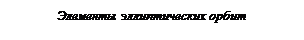1. Наклонение i плоскости орбиты к плоскости эклиптики. Может иметь значения от 0º до 180º. Если 0º £ i < 90º, то планета движется вокруг Солнца в том же направлении, что и Земля (прямое движение). Если 90º > i > 180º, то планета движется в противоположном направлении (обратное движение).

2. Долгота (гелиоцентрическая) восходящего узла b, т.е. угол между направлениями из центра Солнца на восходящий узел b и на точку весеннего равноденствия. Долгота может иметь значения от 0º до 360º.

Долгота восходящего узла и наклонение определяют положение плоскости орбиты в пространстве.

3. Угловое расстояние w перигелия от узла, т.е. угол между направлениями из центра Солнца на восходящий узел и на перигелий П. Отсчитывается в плоскости орбиты планеты в направлении её движения и может иметь любые значения от 0º до 360º.

Угловое расстояние w определяет положение орбиты в её плоскости.

4. Большая полуось а эллиптической орбиты, которая однозначно определяет сидерический период обращения Т планеты. Среднее суточное движение n = 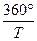, т.е. средняя угловая скорость планеты в сутки.

5. Эксцентриситет орбиты е = , (1)

где а и b - полуоси эллиптической орбиты. Большая полуось а и е определяют размеры и форму орбиты.

6. Момент прохождения через перигелий t ₀, или положение планеты на орбите в какой-то определённый момент времени t.

Зная момент прохождения через перигелий t ₀ и другие элементы орбиты, можно определить положение планеты в плоскости её орбиты для любого момента времени t.

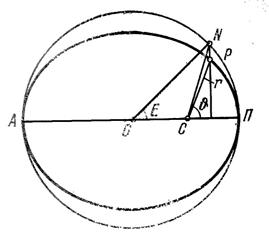
Положение планеты на орбите определяется двумя величинами: радиус-вектором 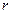и истинной аномалией q. Истинной аномалией планеты называется угол ПСР между направлением из Солнца на перигелий П и радиусом-вектором планеты Р.

r = 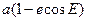, (2)

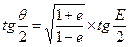, (3)

где Е = < ПОN и называется эксцентрической аномалией.

Эксцентрическая аномалия вычисляется из уравнения Кеплера

М = Е - е sin E, (4)

где М - угол, называемый средней аномалией. Средняя аномалия представляет собой дугу круга, которую бы описала планета за время (t - t ₀), если бы двигалась равномерно по окружности радиуса а со средней угловой скоростью n.

М = n (t - t ₀) = 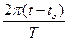. (5)