Электродинамика и распространение радиоволн 3 страница

Поскольку в передающих линиях могут распространяться волны 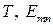и 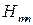типа, то в рассматриваемых резонаторах существуют колебания видов 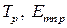и 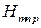. Исходя из граничных условий нетрудно показать, что для колебани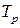й и 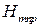индекс 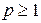, а для .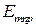

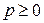Как и в случае волноводов, в качестве элементов связи с объемными резонаторами, применяют электрические вибраторы (штыри), магнитные вибраторы (петли, рамки), а также отверстия связи (щели).

Зная структуру требуемого колебания в резонаторе, легко выбрать ориентацию возбуждающего штыря или рамки. Так, если наводимая в штыре величина ЭДС равна:

,

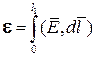где 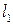− длина штыря, то максимальная ЭДС, а значит, и наибольшие токи в штыре будут протекать в том случае, когда штырь находится в пучности электрического тока и ориентирован вдоль линий электрического поля.

ЭДС, наводимая в рамке, равна:

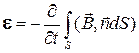, (3.6)

где 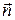− нормаль к плоскости рамки, 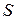− площадь рамки. Отсюда следует, что наибольшая ЭДС будет наводиться, если рамка находится в пучности магнитного поля, а плоскость рамки перпендикулярна магнитным силовым линиям.

Отверстие связи следует прорезать в таком месте объемного резонатора, где оно пересекается линиями поверхностного тока в стенках резонатора, т. е. там, где существует максимум нормальной к плоскости отверстия электрической составляющей либо максимум касательной к плоскости отверстия составляющей магнитного поля.

Проходной объемный резонатор

Основным элементом, на основе которого строятся многие типы волноводных полосовых фильтров, является объемный резонатор, образованный двумя плоскими неоднородностями, расположенными на расстоянии 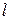друг от друга по обе стороны отрезка линии передачи. Такими неоднородностями могут быть индуктивные или емкостные диафрагмы, реактивные штыри и т. д. Определим частотную характеристику резонатора, т. е. зависимость мощности, поступающей в нагрузку, включенную на выходе резонатора, от частоты.

Электрические параметры резонатора удобно характеризовать параметрами рассеяния. При использовании концепции падающих и отраженных волн для четырехполюсника (а проходной объемный резонатор является двухплечим устройством – четырехполюсником) можно записать следующее (см. рис. 3.1):

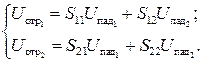(3.7)

Рис. 3.1. Падающие и отраженные волны на клеммах четырехполюсника.

Коэффициенты 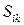исследуемого четырехполюсника запишем в виде матрицы рассеяния:

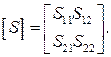(3.8)

В общем случае все элементы 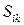− комплексные величины:

,

где 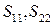− коэффициенты отражения соответственно для плеча 1 слева и для плеча 2 справа; 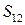− коэффициент передачи от плеча 1 к плечу 2; 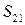− коэффициент передачи от плеча 2 к плечу 1.

Рассмотрим случаи, когда на входе и выходе стоят одинаковые неоднородности (например, две одинаковые диафрагмы). Пренебрегая потерями энергии в неоднородностях, записываем формулу:

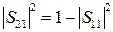(3.9)

Пусть на вход резонатора поступает падающая волна с амплитудой 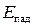. Тогда часть энергии падающей волны отразится от первой неоднородности, а часть пройдет в резонатор:

; .

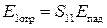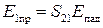Прошедшая волна 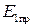распространяется по резонатору, доходит до второй неоднородности, получив фазовый сдвиг β l, частично отражается от нее и, еще раз пройдя резонатор, возвращается от первой неоднородности с фазовым сдвигом 2β l, частично проходит через нее и создает вторую отраженную волну на входе резонатора:

.

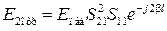Проводя аналогичные рассуждения для волн внутри резонатора, можно показать, что на входе резонатора будет бесконечное количество отраженных волн, а на выходе – прошедших.

Суммируя все отраженные волны, получаем:

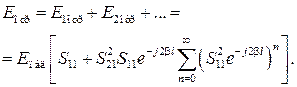(3.10)

Аналогично получаем суммарное поле на выходе резонатора:

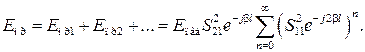(3.11)

При 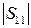< 1 ряды (3.10) и (3.11) представляют собой бесконечно убывающие геометрические прогрессии. Просуммировав эти ряды, получим выражения для результирующего коэффициента отражения на входе 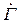и для коэффициента передачи резонатора :

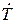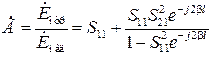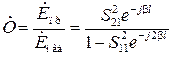; . (3.12)

Подставив (3.9) в (3.12), получим:

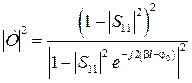, (3.13)

где 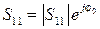, φ ₀ – начальная фаза.

Из (3.13) следует, что вся энергия падающей волны поступает на выход резонатора, т. е. 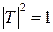, когда выполняется условие:

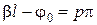, (3.14)

где 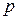=0, 1, 2, 3...

Подставив в (3.14) 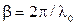, найдем длину резонатора, т. е. длину, при которой :

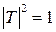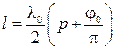, (3.15)

где λ ₀ − длина волны в линии передачи.

Только на частоте 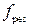– резонансной частоте резонатора, когда выполняется условие (3.14), выполняется и условие 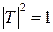. При отклонении от этой частоты амплитуда прошедшей волны уменьшается.

При 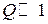нагруженную добротность резонатора можно определить по общепринятой формуле [2]:

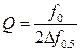, (3.16)

где Δ f _{0, 5} – расстройка от частоты f _рез, при которой мощность на выходе резонатора уменьшается в два раза по отношению к ее максимальному значению. Величину Δ f _{0, 5} еще называют полушириной резонансной линии и измеряют по уровню прохождения половины от максимальной передаваемой на выход резонатора мощности, т.е. по уровню -3 дБ (см. рис. 3.2).

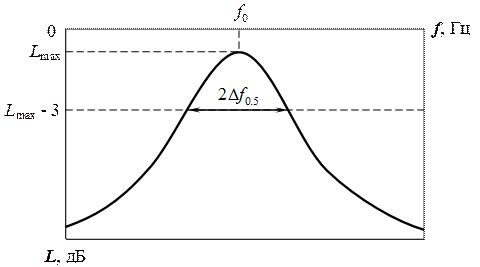
Рис. 3.2. Амплитудно-частотные характеристики объемного резонатора, включенного в режиме «на проход», вблизи резонансной частоты.

На рис. 3.2. буквой L обозначена амплитудно-частотная характеристика (АЧХ) прямых потерь в резонаторе, которая связана с падающей на вход резонатора и прошедшей на его выход мощностям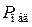и ( и 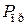соответственно) формулой:

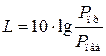, (3.17)

Собственную добротность прямоугольного объемного резонатора с колебанием H ₁₀₁ при отсутствии в нем диэлектрических потерь можно рассчитать по формуле [3]:

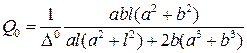, (3.18)

где a, b и l − внутренние размеры полости резонатора; 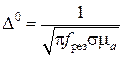− глубина проникновения электромагнитной волны в металл или, иначе говоря, глубина скин-слоя.

Добротность связи 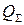, о которой говорится в формуле (3.3), теоретически рассчитать сложно. Поэтому на практике, как правило, ее определяют косвенно по формуле (3.3), предварительно экспериментально определив нагруженную добротность с использованием формулы (3.16) и рассчитав собственную добротность резонатора по формуле (3.18).

В настоящей работе для измерения амплитудно-частотных характеристик применяется измеритель модуля коэффициента передачи и отражения «Р2М-18» российской фирмы «Микран» (г. Томск). Схема измерения АЧХ исследуемых объемных резонаторов представлена на рис. 3.3.

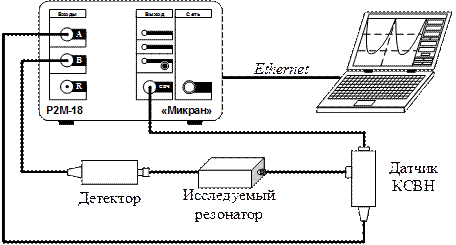
Рис. 3.3. Схема измерения амплитудно-частотных характеристик МПР
с помощью прибора «Р2М-18».

Входной сигнал, пропорциональный уровню мощности (отраженной – при измерении модуля коэффициента отражения; падающей – при измерении модуля коэффициента передачи) СВЧ-колебаний, оцифровывается и считывается процессором цифровой обработки сигналов измерителя, который, выполнив все необходимые вычисления, передаёт результаты в ЭВМ. Контроль и измерение амплитудно-частотных характеристик резонатора осуществляется на мониторе компьютера с помощью частотных меток.

Для устранения потерь, вносимых трактом, непосредственно перед измерением необходимо провести калибровку СВЧ-тракта.

В качестве исследуемого резонатора на усмотрение преподавателя может быть использован прямоугольный, цилиндрический, либо микрополосковый резонаторы.

Порядок выполнения работы

Получив у преподавателя допуск и резонатор для исследований, приступить к выполнению лабораторной работы в следующем порядке:

1. Определить резонансную частоту резонатора 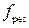для низшего колебания по его геометрическим размерам.

2. Для прямоугольного резонатора определить его собственную добротность на частоте низшего колебания согласно расчету с учетом того, что резонатор выполнен из меди.

3. Ознакомиться с устройством и назначением измерительной аппаратуры. Проверить правильность соединений приборов по схеме.

4. Включить аппаратуру в сеть согласно инструкции. Прогреть не менее 15 минут.

5. Произвести калибровку СВЧ-тракта, после чего включить исследуемый резонатор в схему измерения АЧХ согласно рис. 3.3.

6. Снять амплитудно-частотные характеристики резонатора (прямые и обратные потери) во всем рабочем диапазоне прибора «Р2М-18».

7. С помощью частотных меток на мониторе компьютера измерить частоту низшего колебания резонатора, ширину полосы пропускания по уровню -3 дБ вблизи этой частоты и рассчитать нагруженную добротность резонатора по формуле (3.16).

8. Рассчитать добротность связи резонатора на частоте низшего колебания.

9. Отметить, какие еще моды колебаний присутствуют на спектре, и измерить их частоты. По измеренным значениям частот определить названия этих мод.

Содержание отчета

1. Схема лабораторной установки.

2. Чертеж исследуемого резонатора с указанием всех его геометрических размеров.

3. Расчет резонансной частоты для низшего колебания и его собственной добротности на этой частоте.

4. Результаты измерений АЧХ прямых и обратных потерь в резонаторе с указанием названий всех обнаруженных типов колебаний.

5. Расчет добротности связи на частоте низшего колебания.

6. Краткая сводка результатов всех проведенных измерений и расчетов.

7. Выводы по полученным результатам.

Контрольные вопросы

1. Что такое резонаторы? Где они применяются?

2. Определение низшего типа колебаний.

3. Что такое добротность резонатора? Как она определяется?

4. Какие параметры резонатора определяют спектр его резонансных частот?

5. Как на СВЧ реализуется эквивалентная схема в виде параллельного контура?

6. Как на СВЧ реализуется эквивалентная схема в виде последовательного контура?

7. Какие параметры являются для резонаторов основными?

8. Чем определяется существование определенного типа колебаний в резонаторе?

9. Чему равна длина волны в прямоугольном резонаторе?

10. Нарисовать структуру поля H ₁₀₁ в прямоугольном резонаторе.

11. Нарисовать структуру поля в открытом коаксиальном резонаторе длиной .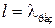

12. Нарисовать схемы возбуждения резонаторов.

13. От чего зависит коэффициент передачи резонатора при заданной собственной добротности?

14. От чего зависит собственная добротность резонатора?

15. Какой из полых резонаторов (шаровой, цилиндрический, прямоугольный или коаксиальный) имеет большую собственную добротность при одинаковом объеме и на одной и той же частоте?

17. Какие колебания в резонаторе называются вырожденными?

18. Как можно изменять степень связи резонатора с возбуждающей щелью?

Лабораторная работа № 4

ЭЛЕМЕНТАРНАЯ МАГНИТНАЯ АНТЕННА

Цель работы: Изучение свойств элементарной магнитной антенны и измерение ее диаграммы направленности.

Краткие теоретические сведения

Элементарной магнитной антенной называют прямолинейный возбуждаемый магнитным током излучатель, длина которого много меньше длины волны возбуждаемого им поля. В связи с этим модуль и фаза линейной плотности магнитного тока распределены по длине такой антенны равномерно. При этом фиктивный магнитный ток и заряды на антенне изменяются по гармоническим законам.

Простейшей моделью элементарного магнитного излучателя является плоская проводящая рамка (одиночный виток провода) с электрическим линейным гармоническим током, периметр которой весьма мал по сравнению с длиной волны создаваемого поля. Такой излучатель называют элементарной электрической рамкой. Очевидно, что эквивалентный такой рамке фиктивный элементарный магнитный излучатель ориентирован перпендикулярно плоскости рамки.

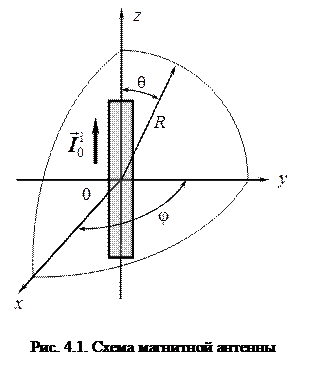
Рассмотрим излучение магнитной антенны. Начало сферической системы координат располагается в середине антенны, при этом полярная ось (ОZ) направлена вдоль ее оси (рис. 4.1). Величина линейного магнитного тока в антенне равна:

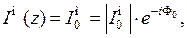(4.1)

где 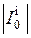− амплитуда, а Φ ₀ − фаза тока, не зависящие от координаты z
(рис. 4.2).

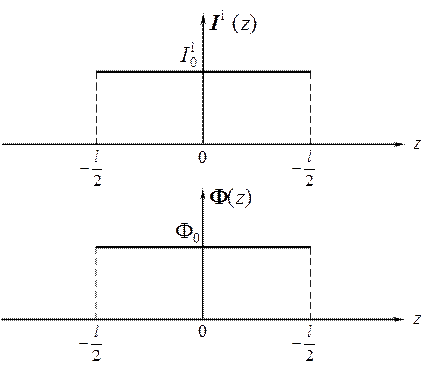
Рис. 4.2. Эпюры тока и фазы в элементарной магнитной антенне.

Найдем комплексную амплитуду векторного магнитного потенциала 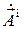, создаваемого магнитным током, по известной интегральной формуле [1]:

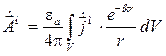, (4.2)

где 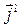− комплексная амплитуда плотности магнитного тока; 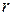− расстояние между точкой наблюдения (точка, где определяется значение векторного потенциала) и точкой интегрирования (точка, где в текущий момент находится элемент тока на поверхности излучателя) согласно рис. 4.3.

Если расстояние между точками наблюдения и интегрирования представить в виде 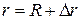, то при любом положении точки наблюдения будет выполняться соотношение 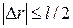. Учитывая, что 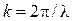и 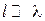, имеем 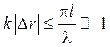. Тогда экспоненциальную функцию в выражении (4.2) можно представить в виде:

.

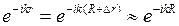Если далее ограничиться такими точками наблюдения, для которых выполняется неравенство 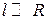, расстояние 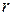, входящее в знаменатель (4.2), можно приближенно заменить постоянным значением R. Далее вынесем фазовый множитель 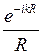из-под интеграла и получим:

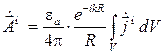. (4.3)

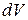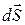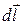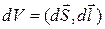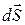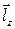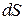Элемент объема представим в виде скалярного произведения элемента площади поперечного сечения антенны на элемент длины антенны : . Вектор определяется как произведение на , где 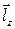− единичный орт, направленный вдоль длины антенны по оси z.

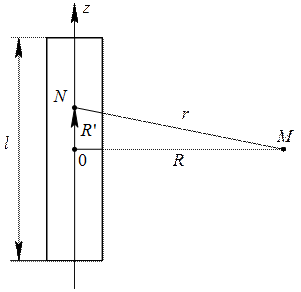
Рис. 4.3. Схема для расчета векторного магнитного потенциала:
M (r, θ, φ) − точка наблюдения; N (r, θ, φ) − точка интегрирования;
r − расстояние между точками интегрирования и точкой наблюдения;
0 – центр координат.

Поскольку векторы 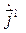и 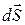параллельны, их скалярное произведение равно величине магнитного тока 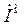в антенне:

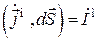. (4.4)

Следовательно, можно записать:

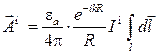. (4.5)

Учитывая, что 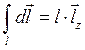, получим окончательное выражение для комплексной амплитуды векторного магнитного потенциала антенны:

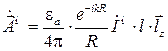. (4.6)

Из (4.6) следует, что векторный магнитный потенциал элементарной магнитной антенны в точке наблюдения направлен параллельно ее оси и зависит от расстояния R, представляющего радиальную координату точки наблюдения в сферической системе координат, начало которой совпадает с центром излучателя.

Найдем составляющие электромагнитного поля, создаваемого элементарной магнитной антенной. Из определения 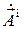следует:

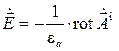. (4.7)

Используя выражение (4.7), рассчитаем напряженность электрического поля магнитной антенны. Вычислив значение ротора векторного магнитного потенциала в сферической системе координат, получим:

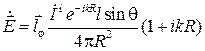. (4.8)

Напряженность магнитного поля антенны определим по второму уравнению Максвелла для комплексных амплитуд:

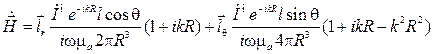. (4.9)

Зависимость поля от координаты R в точке наблюдения позволяет разбить окружающее излучатель пространство на три зоны – ближнюю, промежуточную и дальнюю. Ближняя зона индукции характеризуется такими расстояниями R, для которых справедливо следующее неравенство: 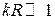. В связи с этим для ближней зоны в выражениях (4.8) и (4.9) остаются только те слагаемые, которые содержат 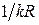в высшей степени. Для этой зоны также будет справедливо соотношение .

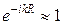Промежуточная зона является переходной между ближней и дальней и характеризуется соотношением 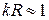. В этом случае в выражениях (4.8) и (4.9) учитываются все слагаемые.

Дальняя зона характеризуется расстояниями, для которых 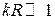. В связи с этим в выражениях (4.8) и (4.9) следует учитывать только члены, содержащие kR в высшей степени. Таким образом, в дальней зоне выражения для составляющих электромагнитного поля антенны будут следующими:

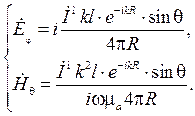
Рассмотрим аналог элементарной магнитной антенны, представляющей собой пластину шириной d и длиной l, причем 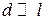. Допустим, что вдоль этой пластины по обеим ее сторонам протекает сторонний магнитный ток, поверхностная плотность которого постоянна вдоль длины пластины и равна 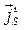. Тогда магнитный ток, протекающий по обеим сторонам пластины и создающий электромагнитное поле, будет равен: 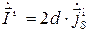. Электромагнитное поле, создаваемое током 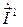, можно рассчитать, используя выражения (4.8) и (4.9). Соответствующая структура поля показана на рис. 4.4.

Рассмотрим граничные условия, которые будут удовлетворять этому случаю. В пределах пластины 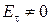, 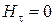. За пределами пластины – наоборот, 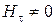, 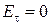. В соответствии с граничными условиями .
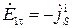В связи с этим, магнитный ток, протекающий по пластине, запишем в виде:

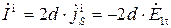. (4.10)

Построим физическую систему, отвечающую граничным условиям, показанным на рис. 4.4. За пределами пластины 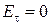и 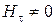. Подобные граничные условия справедливы для поверхности идеального металла. Если поместить лист идеального металла за пределами периметра пластин антенны в плоскости рисунка, то записанные выше граничные условия будут соблюдаться. Для выполнения другой пары граничных условий (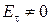, 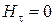) сделаем в листе идеального металла щель, конфигурация и размеры которой совпадают с размерами и формами пластины. К краям щели подведем от генератора переменное напряжение. Полагая, что напряженность электрического поля в зазоре щели постоянна, можно записать: 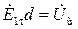, где 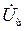– создаваемая генератором переменная разность потенциалов. Тогда комплексная амплитуда магнитного тока согласно выражению (4.10) будет равна: .

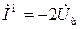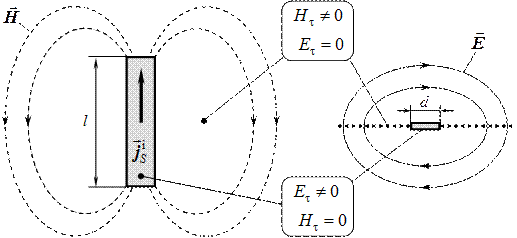
Рис. 4.4. Граничные условия.

Таким образом, физическим аналогом магнитного тока в случае щелевой (магнитной) антенны является двойная разность потенциалов между краями щели. Как показывают многочисленные исследования, концепция магнитного тока оказывается удобной при анализе различных антенн щелевого типа. Хотя, стоит помнить, что в реальности никаких магнитных токов не существует, – их вводят для удобства анализа электромагнитных процессов чисто гипотетически.

Мощность излучения магнитной антенны и ее сопротивление излучения определяются формулами:

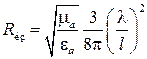, . (4.11)

Диаграмма направленности (ДН) магнитной антенны в плоскости, перпендикулярной ее полярной оси и проходящей через ее центр, т.е. в экваториальной или, еще можно сказать, азимутальной плоскости, представляет собой окружность, центр которой совпадает с началом координат. Иначе говоря, в этой плоскости антенна излучает одинаково во всех направлениях. В меридиональной плоскости диаграмма направленности антенны представляет собой две окружности одинакового радиуса, имеющие одну общую точку, совпадающую с началом координат. Центры этих окружностей будут лежать в экваториальной плоскости по обе стороны от оси антенны. Таким образом, в пространстве диаграмма направленности магнитной антенны представляет собой тороид, ось которого, совпадает с полярной осью антенны.

Порядок выполнения лабораторной работы