Принцип инерциального счисления пути

Инерциальные навигационные системы (ИНС) основаны на измерении ускорений ВС по осям системы координат. Ускорения измеряются устройствами, называемыми акселерометрами. Принцип действия акселерометра основан на свойстве инерции. В упрощенном виде акселерометр представляет собой трубку с расположенным внутри нее грузом в виде шарика (рис. 8.15). Если трубка движется с ускорением, направленным по ее оси, то груз вследствие своей инерции смещается в сторону, противоположную ускорению. Смещение тем больше, чем больше ускорение. Если ускорение прекращается, пружина возвращает груз в нулевое положение. Таким образом, измеряя смещение, можно измерять ускорение.

Современные акселерометры обладают высокой чувствительностью и могут измерить ускорение, составляющее одну миллионную от ускорения свободного падения. Если бы тело из состояния покоя начало движение с таким ускорением, то оно сдвинулось бы на один миллиметр лишь через 15 секунд.

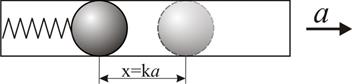
Рис. 8.15. Акселерометр

Два акселерометра расположены в горизонтальной плоскости и ориентированы на север-юг и восток-запад. Они предназначены для измерения ускорений по этим направлениям. Третий расположен вертикально (рис. 8.16).

Из физики и математики известно, что ускорение является производной от скорости, то есть характеризует быстроту ее изменения. Соответственно, скорость – это производная расстояния. Операцией, обратной дифференцированию (взятию производной), является интегрирование. Следовательно, если значение производной (измеренное ускорение) известно, то после его интегрирования получим скорость, а после интегрирования скорости получим пройденное расстояние (рис. 8.17).

Рис. 8.16. Счисление в сферической системе координат

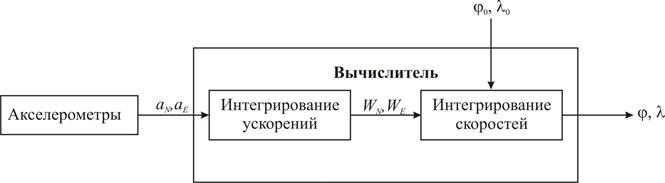
Рис. 8.17. Упрощенная блок-схема инерциального счисления

Пусть a_N и a_E – измеренные ускорения по направлениям на север и восток, W_N и W_E – составляющие путевой скорости, S_N и S_E – пройденные расстояния по этим же направлениям. Тогда

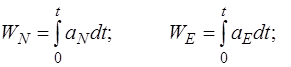(8.4)

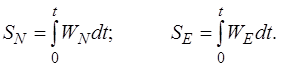(8.5)

Современные ИНС осуществляют счисление в географической системе координат, то есть определяют широту и долготу. Если принять Землю за сферу, то текущие широта φ и долгота λ (в радианах) могут быть определены как:

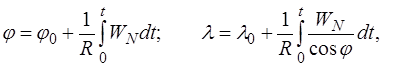(8.6)

где R – радиус Земли,

φ ₀, λ ₀ – начальные координаты ВС.

Интегрирование и все прочие расчеты выполняются входящими в состав ИНС цифровыми вычислителями (микропроцессорами).

Таким образом, как бы ни был ориентирован самолет в пространстве, то есть, какими бы ни были курс, крен и тангаж, для счисления пути должны использоваться ускорения в системе координат, жестко связанной с Землей. В зависимости от того, каким образом обеспечивается выполнение этого условия, ИНС можно разделить на две группы:

- основанные на использовании гироплатформы (будем их называть традиционными ИНС),

- бесплатформенные ИНС.

Первыми в 40-е годы ХХ века были разработаны и на протяжении пятидесяти лет совершенствовались традиционные ИНС. В этих системах акселерометры установлены на основе, называемой гироплатформой. Гироплатформа на протяжении всего полета должна располагаться строго горизонтально и ориентирована по направлению меридиана. В этом случае акселерометры независимо от поворотов ВС всегда ориентированы по осям системы координат, связанной с Землей − один акселерометр ориентирован на север, второй на восток и третий вверх.

Гироплатформа удерживается в нужном положении с помощью гироскопов – в принципе таких же, которые рассматривались в главе о гироскопических курсовых приборах, но гораздо более точных, имеющих малый собственный уход.

В последней четверти прошлого века стали развиваться бесплатформенные ИНС, которые не совсем корректно называют системами на лазерных гироскопах. В этих системах акселерометры жестко закреплены на самолете, ориентированы по его строительным осям и, естественно, вращаются вместе с ним, измеряя ускорения вдоль осей самолета. Значения же ускорений по осям земной системы координат получаются расчетным путем.

Для наглядности в данной главе работа инерциальных систем будет рассмотрена на примере традиционных ИНС, имеющих в своем составе гироплатформу. Бесплатформенные ИНС будут рассмотрены далее.

Инерциальные навигационные системы обладают рядом достоинств и преимуществ перед другими навигационными системами.

1. Автономность. ИНС не требуют для своей работы установки какого-либо наземного оборудования. Все, что необходимо для счисления пути, находится на борту.

2. Широкая область возможного применения. ИНС, в отличие от некоторых других систем, могут использоваться практически над всей территорией земного шара, включая и полярные районы, а также под водой и в космосе.

3. Абсолютная помехозащищенность. Поскольку ИНС основана на использовании свойства инерции тел, не существует естественных и невозможно создать искусственные помехи работе системы. Современная наука пока не знает способа, которым можно было бы заставить акселерометр на летящем ВС измерить неправильное ускорение.

4. Возможность измерения всех основных параметров, необходимых для навигации.

Перечисленные достоинства и определили широкое использование ИНС на воздушных и морских судах, космических аппаратах, баллистических и крылатых ракетах.

Разумеется, у ИНС имеются и недостатки, большая часть которых, впрочем, свойственна не только инерциальным, но и любым системам счисления пути. К ним относятся необходимость знания начальных координат, возрастание погрешностей счисления со временем полета и вытекающая отсюда необходимость коррекции координат.

Еще 15-20 лет назад применительно к традиционным ИНС можно было бы отметить в качестве недостатков невысокую точность счисления, сложность и низкую надежность системы, громоздкость и высокую стоимость. Эти недостатки были связаны с необходимостью использования высокопрецизионных, дорогих и сложных гироскопов, с помощью которых гироплатформа должна удерживаться в заданном положении.

Но с появлением бесплатформенных ИНС ситуация быстро изменилась. ИНС стали меньше по размерам, проще, дешевле. А со временем они обогнали традиционные ИНС и по точности.

Погрешности ИНС. Как и любая система счисления пути ИНС имеет погрешности, вызванные, с одной стороны, неточной установкой начальных координат, а с другой, – неточным измерением параметров движения. Как и у любой системы счисления погрешности определения координат возрастают на протяжении полета.

Казалось бы, основной причиной неточности ИНС должны быть погрешности измерения акселерометрами ускорений. Но, как уже отмечалось, современные акселерометры достаточно точны и вовсе не они являются основной проблемой. В традиционных ИНС наибольший вклад в общую погрешность вносит собственный уход гироскопов, стабилизирующих платформу. Этот уход гораздо меньше собственного ухода гироскопических курсовых приборов и составляет доли градуса в час, однако и это приводит к существенным погрешностям. Ведь в результате такого ухода оси акселерометров оказываются неточно направленными по осям системы координат (по меридиану и параллели), и измеренные ускорения не соответствуют фактическим ускорениям по этим направлениям. Чем дольше длится полет, тем больше уходит гироплатформа, тем больше погрешности измерения ускорений, а, следовательно, и скоростей, и координат.

Но у погрешностей ИНС, в отличие от других систем счисления, есть характерная интересная особенность – погрешности возрастают неравномерно. Рассмотрим, почему это происходит.

Допустим, что при горизонтировании гироплатформа была выставлена неточно и составляла угол ν к плоскости горизонта (рис. 8.22).

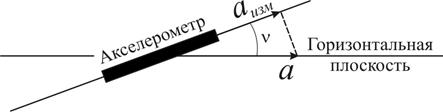
Рис.8.22. Погрешность из-за неточного горизонтирования

В этом случае вместо фактического ускорения a будет измерена его проекция на ось акселерометра a_изм. Следовательно, ускорение будет измерено с погрешностью Δ a=a_изм − a.

Из-за этой погрешности после интегрирования измеренного ускорения с погрешностью Δ W будет рассчитана скорость, а после интегрирования скорости и пройденное расстояние будет рассчитано с погрешностью Δ S.

Но ведь с помощью этого расстояния, как было показано, определяется угол θ, на который необходимо довернуть гироплатформу для приведения ее в правильное положение. Следовательно, и этот угол будет рассчитан неточно, платформа будет повернута не на тот угол, на который необходимо. Угол ν, под которым первоначально гироплатформа была наклонена к горизонту, изменится. Соответственно изменится и погрешность измерения ускорения, расчета скорости, пройденного расстояния, что снова приведет к изменению угла установки платформы ν. Получается замкнутый круг, в котором изменение всех величин взаимосвязано.

Процесс изменения в полете угла ν может быть описан дифференциальным уравнением, которое здесь не приводится. Решением этого уравнения является периодическая синусоидальная функция. Это означает, что наклон гироплатформы к горизонту будет в процессе полета меняться по синусоиде, то есть становиться то больше, то меньше. Период этой функции составляет T_ш=84, 4 минуты и называется периодом Шулера в честь немецкого инженера Максимиллиана Шулера (1882-1972). Величина периода Шулера является константой для нашей планеты, поскольку она зависит только от радиуса Земли и ускорения свободного падения g. Если представить себе маятник с нитью длиной, равной радиусу Земли, то он имел бы период колебаний T_ш. Такой же период обращения имел бы искусственный спутник Земли, если бы его удалось пустить на нулевой высоте над самой поверхностью планеты. На самом деле это сделать, конечно, невозможно из-за наличия атмосферы.

С таким же периодом Шулера, с которым меняется угол наклона гироплатформы, будут изменяться и погрешности измерения ускорений, скоростей, расстояний. Таким образом, погрешности будут возрастать из-за ухода гироскопов, но также иметь и периодическую составляющую (рис. 8.23).

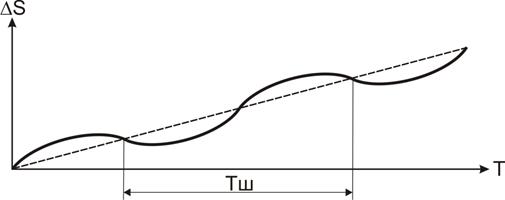
Рис. 8.23. Период Шулера

Вследствие возрастания погрешностей инерциальные системы, как и любые системы счисления пути, требуют периодической коррекции счисленных координат с помощью более точных технических средств.

У современных ИНС средняя квадратическая погрешность определения координат составляет 3-4 морских мили за 10-11 ч полета (без коррекции).