Метод градиентного спуска

Рассмотрим функцию f считая для определенности, что она зависит от трех переменных х, у, z. Вычислим ее частные производные df/dx, df/dy, df/dz и образуем с их помощью вектора, который называют градиентом функции:

Здесь i, j, k - единичные векторы, параллельные координатным осям. Частные производные характеризуют изменение функции по каждой независимой переменной в отдельности. Образованный с их помощью вектор градиента дает общее представление о поведении функции в окрестности точки (x, y, z). Направление этого вектора является направлением наиболее быстрого возрастания функции в данной точке. Противоположное ему направление, которое часто называют антиградиентным, представляет собой направление наиболее быстрого убывания функции. Модуль градиента

определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке (x, y, z) меньше модуля градиента. При переходе от одной точки к другой как направление градиента, так и его модуль, вообще говоря, меняются. Понятие градиента естественным образом переносится на функции любого числа переменных.

Перейдем к описанию метода градиентного спуска. Основная его идея состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея реализуется следующим образом.

Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции. Специальный выбор направления движения на каждом шаге позволяет надеяться на то, что в данном случае приближение к наименьшему значению функции будет более быстрым, чем в методе покоординатного спуска.

Метод требует вычисления градиента целевой функции на каждом шаге. Если она задана аналитически, то это, как правило, не проблема: для частных производных, определяющих градиент, можно получить явные формулы. В противном случае частные производные в нужных точках приходится вычислять приближенно, заменяя их соответствующими разностными отношениями:

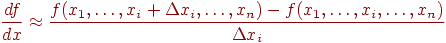
Отметим, что при таких расчетах 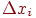, нельзя брать слишком малым, а значения функции нужно вычислять с достаточно высокой степенью точности, иначе при вычислении разности

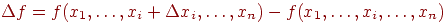
будет допущена большая ошибка.

На рис. 12 изображены линии уровня той же функции двух переменных u=f(x, y), что и на рис. 11, и приведена траектория поиска ее минимума с помощью метода градиентного спуска. Сравнение рис. 11 и рис. 12 показывает, насколько более эффективным является метод градиентного спуска.

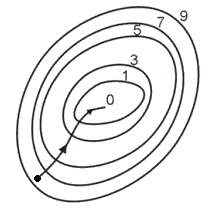
Рис. 11. Поиск наименьшего значения функции методом градиентного спуска.

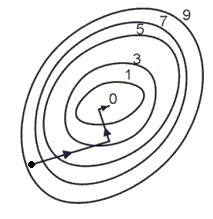
Рис. 12. Поиск наименьшего значения функции методом наискорейшего спуска.

Пример решения задач в MathCAD

Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис. 1 на интервале (-2, 5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В MathCAD с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.

Рис. 13. График функции f (x)=x⁴+5-x³-10-x
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
- Minimize (f, xi,..., х_м) - вектор значений аргументов, при которых функция f достигает минимума;
- Maximize (f, xi,..., х_м) - вектор значений аргументов, при которых функция f достигает максимума;
f (xi,..., х_м,...) - функция;
xi,..., х_м- аргументы, по которым производится минимизация(максимизация).
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис. 1) без дополнительных условий показаны в листингах 2-3. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений х от -∞ до ∞.
Листинг 2. Минимум функции одной переменной

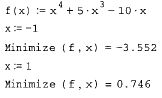
Листинг 3. Максимум функции одной переменной

Условный экстремум
В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. В листинге 4 показаны примеры поиска условного экстремума на различных интервалах, определенных неравенствами. Сравните результаты работы этого листинга с двумя предыдущими.

Листинг 4. Три примера поиска условного экстремума функции

Экстремум функции многих переменных
Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Поэтому ограничимся примером (листинг 5) нахождения максимума и минимума функции, показанной в виде графиков трехмерной поверхности илиний уровня на рис. 2. Привлечем внимание читателя только к тому, как с помощью неравенств, введенных логическими операторами, задается область на плоскости (X, Y).

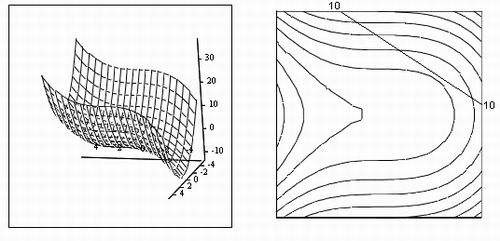
Рис. 14. График функции f (х, у)и отрезок прямой х+у=10
Листинг 5. Экстремум функции двух переменных

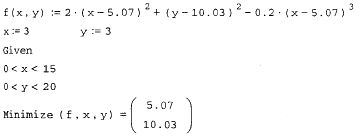
Дополнительные условия могут быть заданы и равенствами. Например, определение после ключевого слова Given уравнения х+у=0 приводит к такому решению задачи на условный экстремум:
Как нетрудно сообразить, еще одно дополнительное условие привело к тому, что численный метод ищет минимальное значение функции f(x, y)вдоль отрезка прямой, показанного на рис. 2.

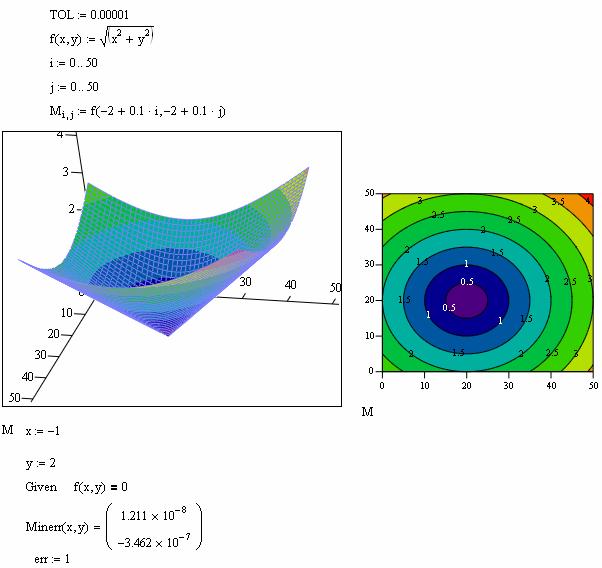
Поиск экстремума функции нескольких переменных c помощью функции Minerr:

· x₁: =C₁,..., х_м: =С_м — начальные значения для неизвестных;

· Given — ключевое слово;

· система алгебраических уравнений и неравенств, записанная логическими операторами;

· Minerr (x₁,..., х_м) — приближенное решение системы относительно переменных x_1, ..., х_м, минимизирующее невязку системы уравнений.

Задание:

1. Внимательно изучите предложенный Вам материал и составьте конспект.

2. Ответьте на следующие вопросы:

2.1. Дайте определение функции нескольких переменных.

2.2. Приведите пример функции нескольких переменных.

2.3. Что называется пределом функции нескольких переменных и как обозначается?

2.4. Дайте определение частной производной функции нескольких переменных.

2.5. Что называется экстремумом функции?

2.6. Перечислите необходимый и достаточный признаки существования экстремума функции нескольких переменных.

2.7. Когда применяются приближённые методы нахождения экстремумов функций двух переменных?

2.8. Перечислите известные Вам приближённые методы нахождения экстремумов функций двух переменных.

2.9. В чём заключается приближённый методХука – Дживса и каков алгоритм его выполнения?

2.10. В чём заключается приближённый методполного перебора?

2.11. Опишите метод покоординатного спуска, каковы достоинства и недостатки данного метода.

2.12. Опишите метод градиентного спуска, какова его основная идея, достоинства и недостатки данного метода по сравнению с методом покоординатного спуска.

Список рекомендуемой литературы:

1. Банди Б. Методы оптимизации. Вводный курс, с. 58-60

2. Губарь Ю.В. Введение в математическое программирование, //www.intuit.ru/department/mathematics/mathprog/10/

3. //www.intuit.ru/department/mathematics/mathprog/10/