
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Загальна модель прийняття рішень з очікуваною корисністю.
|
|
Як надходить підприємець, коли необхідно прийняти рішення - ризикувати чи ні?
Щодо одержуваного середнього виграшу зазначені альтернативи практично еквівалентні, і якщо гравець байдужний до ризику, він зволіє ризикнути, якщо ж він до ризику не байдужна, (а переважна більшість людей саме такі), те вибір буде залежати головним чином від фінансового стану гравця. Гравці, що мають скромний грошовий дохід W зволіють не ризикувати й виберуть гарантований виграш.
Для особи приймаюче рішення (ЛПР), що володіє великим капіталом, коли програш не великий у порівнянні зі своїм капіталом, переважніше буде ризикнути.
Ризикувати будуть також гравці патологічно схильні до азартних авантюр.
Американськими вченими Нейманом і Моргенштерном було показано, що особа приймаюче рішення (ЛПР) при ухваленні рішення буде прагнути до максимально очікуваної корисності, тобто із всіх можливих рішень він вибере те, що забезпечує найбільшу очікувану корисність.
Корисність (W)- це деяке число, приписуване ЛПР кожному можливому результату.
Функція корисності Неймана - Моргенштейна (U(W)) показує корисність, що приписує ЛПР кожному можливому результату.
Причому в кожного ЛПР своя функція корисності, що показує його перевагу до тих або іншим исходам у залежності відносини до ризику.
Як ми вже говорили, якщо гравець до ризику не байдужний, то вибір буде залежати головним чином від фінансового стану гравця.
Очікувана корисність події дорівнює сумі добутків імовірностей исходов на значення корисності цих ісходів.
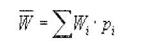
Тому для ухвалення рішення у випадку не байдужності ЛПР до ризику потрібно спочатку оцінити значення полезностей кожного з исходов.
Нейман і Моргенштейн припустили процедуру побудов індивідуальних функцій корисності, які полягають у наступному:
ЛПР відповідає на ряд питань, виявляючи при цьому свої індивідуальні переваги, що враховують його переваги до ризику. Значення полезностей можуть бути знайдені за два кроки:
1. привласнюються довільні значення полезностей виграшу для гіршого й кращого ісходів. Причому гіршому з ісходів ставиться у відповідність менше значення корисності. Корисність навіть для одного індивіда визначається неоднозначно, а з точністю до монотонного перетворення.
2. Гравцеві пропонується на вибір або одержати деяку гарантовану суму W находящуюся в проміжку між s і S
s< W< S
або взяти участь у грі, тобто одержати з імовірністю р найбільшу грошову S і з імовірністю (1-р) одержати найменшу грошову суму s, При. цьому ймовірність варто змінювати (підвищувати або знижувати) доти, поки ЛПР не стане байдужним відносно вибору між одержанням гарантованої суми й грою.
Для цього значенню s приписують довільне значення u(s) а значенню S довільне значення u(S).
Нехай, зазначене значення ймовірності дорівнює р0. Тоді корисність гарантованої суми (очікувана корисність визначається як середнє значення (математичне очікування корисності найбільшої й найменшої сум) визначається по формулі:
u (x)= pu (S) +(1- p)u(s).