Проверка значимости коэффициентов регрессии и коэффициента корреляции

Поскольку анализ взаимосвязей между явлениями проводят в выборочной совокупности, а данные необходимо обобщить на всю генеральную совокупность, то необходимо проверить коэффициенты уравнения регрессии на статистическую значимость.

При объеме выборки меньше или равном 30 единицам значимость коэффициентов уравнения регрессии определяют с помощью t-критерия Стьюдента, который находится по формуле (для коэффициента a):

,

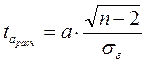где a – коэффициент уравнения регрессии;

n – число единиц совокупности;

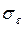- остаточное среднее квадратическое отклонение, которое отображает вариацию результативного признака (y) от всех прочих, кроме факторного признака (x), которое находится по формуле:

,

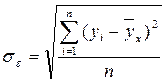где y_i – эмпирические значения результативного признака;

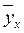- теоретические значения результативного признака, найденные по уравнению регрессии;

n – число единиц в совокупности.

Проверка значимости для коэффициента b осуществляется по формуле:

,

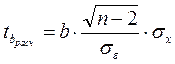где b – коэффициент уравнения регрессии;

n – число единиц совокупности;

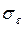- остаточное среднее квадратическое отклонение, которое отображает вариацию результативного признака (y) от всех прочих, кроме факторного признака (x);

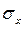- среднее квадратическое отклонение факторного признака, которое находится по формуле:

,

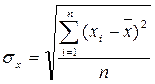где x_i – эмпирические значения факторного признака;

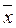- среднее значение факторного признака.

Проведем проверку коэффициентов уравнения регрессии (a=37, 394 и b=0, 026) на статистическую значимость.

Таблица 8 – Проверка значимости коэффициентов регрессии

№ п/п	Кредитные вложения, хi	Прибыль, уi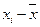
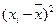
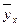
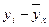
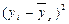
						-28
					51, 6	-16, 6	275, 56
					52, 3	162, 7	26471, 29
					61, 5	34, 5	1190, 25
					52, 7	15, 3	234, 09
					55, 6	-50, 6	2560, 36
					70, 3	66, 7	4448, 89
					51, 9	-47, 9	2294, 41
			-257		41, 3	59, 7	3564, 09
			-196		42, 9	41, 1	1689, 21
			-288		40, 5	6, 5	42, 25
			-162		43, 8	34, 2	1169, 64
						-26
					59, 2	-40, 2	1616, 04
			-172		43, 5	-32, 5	1056, 25
			-256		41, 3	25, 7	660, 49
		0, 5	-278		40, 7	-40, 2	1616, 04
					48, 9	-25, 9	670, 81
			-218		42, 3	6, 7	44, 89
			-334		39, 3	-14, 3	204, 49
		-9				-70
			-264		41, 1	17, 9	320, 41
			-339		39, 2	-22, 2	492, 84
			-304		40, 1	-10, 1	102, 01
			-341		39, 1	52, 9	2798, 41
		0, 5	-343		39, 1	-38, 6	1489, 96
		-0, 2	-217		42, 3	-42, 5	1806, 25
			-272		40, 9	-13, 9	193, 21
			-297		40, 3	-20, 3	412, 09
			-282		40, 6	3, 4	11, 56
Итого		1412, 8	-		1425, 3	-	63795, 79

Рассчитаем остаточное среднее квадратическое отклонение результативного признака:

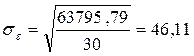
Вычислим t-критерий Стьюдента для коэффициента a уравнения регрессии:

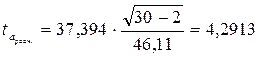
Полученное расчетное значение сравним с табличным:

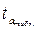(υ =28, α =0, 05) = 2, 0484 < 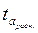= 4, 2913, следовательно, параметр a статистически значим, и его можно распространять на всю совокупность.

Рассчитаем остаточное среднее квадратическое отклонение факторного признака:

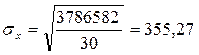
Вычислим t-критерий Стьюдента для коэффициента b уравнения регрессии:

Полученное расчетное значение сравним с табличным:

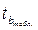(υ =28, α =0, 05) = 2, 0484 > 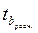= 1, 06, следовательно, параметр b статистически не значим, и его нельзя распространять на всю совокупность.

При объеме выборочной совокупности менее или равном 30 единицам проверка коэффициента корреляции на статистическую значимость осуществляется при помощи t-критерия Стьюдента, который рассчитывается по формуле:

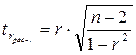
Рассчитаем t-критерий Стьюдента для выборочной совокупности:

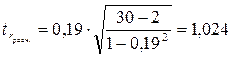
Полученное расчетное значение сравним с табличным:

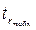(υ =28, α =0, 05) = 2, 0484 > 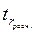= 1, 024, следовательно, коэффициент корреляции признается статистически незначимым.