Листинг программ

Function fnx(x)

fnx = x ^ 3 + 4 * x - 6

End Function

Sub Mpd ()

a = 1

b = 2

e = 0.0001

n = 0

Do

x = (a + b) / 2

f1 = fnx(a)

f2 = fnx(x)

If f1 * f2 > 0 Then

a = x

Else

b = x

n = n + 1

Loop While Abs(b - a) > e

x = (a + b) / 2

Worksheets(" Лист1").Range(" f2").Value = x

Worksheets(" Лист1").Range(" g2").Value = fnx(x)

Worksheets(" Лист1").Range(" h2").Value = n

End Sub

Sub Kasat ()

x = 1

e = 0.0001

n = 0

Do

pr = 3 * x ^ 2 + 4

x1 = x - fnx(x) / pr

c = Abs(x1 - x)

x = x1

n = n + 1

Loop While c > e

Worksheets(" Лист1").Range(" f3").Value = x

Worksheets(" Лист1").Range(" g3").Value = fnx(x)

Worksheets(" Лист1").Range(" h3").Value = n

End Sub

Sub Hord ()

x = 0

e = 0.0001

n = 0

p = 1

Do

x1 = x - fnx(x) * (x - p) / (fnx(x) - fnx(p))

c = Abs(x1 - x)

x = x1

n = n + 1

Loop While c > = e

Worksheets(" Лист1").Range(" f4").Value = x

Worksheets(" Лист1").Range(" g4").Value = fnx(x)

Worksheets(" Лист1").Range(" h4").Value = n

End Sub

Sub Prit ()

x = 1

e = 0.001

n = 0

Do

x1 = (3 - 2 ^ (x)) / 5

c = Abs(x1 - x)

x = x1

n = n + 1

Loop While c > = e

With Worksheets(" Лист1").Range(" f5").Value = x

With Worksheets(" Лист1").Range(" g5").Value = fnx(x)

With Worksheets(" Лист1").Range(" h5").Value = n

End Sub

Для запуска программ нажать на кнопку или на Run.

Полученный результат находится на Листе 1.

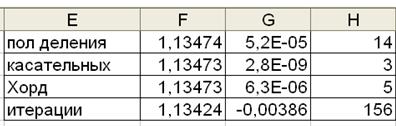
Результаты

Выводы

Если сравнивать сложность алгоритмов рассмотренных выше методов, то все они достаточно просты. Здесь можно выделить метод половинного деления, так как он всегда сходится, если функция непрерывна и имеет корень на рассматриваемом интервале. Это удобно, так как не надо исследовать функцию и выбирать первое приближение для х. Но метод половинного деления требует большего количества итераций, чем другие методы (в данном примере n=14). Время решения уравнений зависит от количества итераций и времени, затрачиваемого на одну итерацию.

Время одной итерации зависит от того, сколько раз вычисляется функция и (если это требуется) её производная на одной итерации. Во всех рассмотренных алгоритмах функция на каждой итерации вычисляется один раз. Но в методе касательных (Ньютона) необходимо вычислить ещё и производную функции. Если сравнивать количество итераций, то все зависит от вида функции. В большинстве случаев меньше всего итераций требует метод касательных (в данном примере еще и метод хорд, где n=5).

Наименьшая погрешность для рассматриваемого примера в методе касательных.

Следовательно, самым точным и быстрым методом для рассматриваемой функции

x²+ 4x – 6 является метод касательных.

Список литературы

1. Лекции по численным методам доцента кафедры химической кибернетики КНИТУ Кошкиной Л.Ю.

2. Кошкина Л.Ю. и др. Вычислительная математика в среде Excel: Методические указания. Часть 2. / Казан. гос. технол. ун-т; Казань, 2003, с. 72

3. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учебное пособие. – М.: Финансы и статистика, 2001.-256 с: ил.

4. Рено Н.Н. Численные методы. Учебное пособие / Казан. гос. технол. университет; Казань, 2007, 112 с.

5. Турчак Л.И. Основы численных методов. - М.: Наука, 1987. – 318 с.

6. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ: Справочник. – М.: Наука.1989. –240 с.

7. Назаров С.В., Мельников П.П. Программирование на MS Visual Basic: Учебное пособие / Под ред. С.В. Назарова. – М.: Финансы и статистика, 2001. – 320 с.: ил.