
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тест Глейсера
|
|
Ще один тест для перевірки гетероскедастичності склав Глейсер. Він запропонував розглядати регресію абсолютних значень залишків 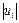 , що відповідають регресії найменших квадратів, як певну функцію від
, що відповідають регресії найменших квадратів, як певну функцію від 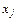 , де
, де 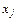 — та незалежна змінна, яка відповідає зміні дисперсії
— та незалежна змінна, яка відповідає зміні дисперсії  . Для цього використовуються такі види функцій:
. Для цього використовуються такі види функцій:
1) 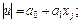
2) 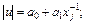
3) 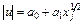 і т.ін.
і т.ін.
Рішення про відсутність гетероскедастичності залишків приймається на підставі статистичної значущості коефіцієнтів 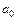 і
і 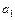 . Переваги цього тесту визначаються можливістю розрізняти випадок чистої і замішаної гетероскедастичності. Чистій гетероскедастичності відповідають значення параметрів
. Переваги цього тесту визначаються можливістю розрізняти випадок чистої і замішаної гетероскедастичності. Чистій гетероскедастичності відповідають значення параметрів 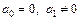 , а змішаній —
, а змішаній — 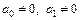 . Залежно від цього треба користуватись різними матрицями S. Нагадаємо, що
. Залежно від цього треба користуватись різними матрицями S. Нагадаємо, що 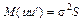 .
.
Приклад 7.4. Нехай потрібно перевірити наявність гетероскедастичності при побудові економетричної моделі, яка описуватиме залежність між доходом і рівнем заощаджень. Вихідні дані наведено в табл.7.4.
Таблиця 7.4
| Місяць | Дохід | Заощадження | Місяць | Дохід | Заощадження |
| 10, 8 | 2, 36 | 17, 5 | 2, 59 | ||
| 11, 4 | 2, 20 | 18, 7 | 2, 90 | ||
| 12, 0 | 2, 08 | 19, 7 | 2, 95 | ||
| 12, 6 | 2, 20 | 20, 6 | 2, 82 | ||
| 13, 0 | 2, 10 | 21, 7 | 3, 04 | ||
| 13, 9 | 2, 12 | 23, 1 | 3, 53 | ||
| 14, 7 | 2, 41 | 24, 8 | 3, 44 | ||
| 15, 5 | 2, 50 | 25, 9 | 3, 75 | ||
| 16, 3 | 2, 43 | 27, 2 | 3, 99 |
Використаємо параметричний тест Гольдфельда — Квандта для встановлення гетероскедастичності при визначенні залежності між наведеними показниками.
Розв’язання. Ідентифікуємо змінні:
Y — заощадження — залежна змінна;
Х — дохід — пояснювальна змінна, Y = f (X).
Крок 1. Вихідна сукупність спостережень упорядковується відповідно до величини елементів вектора Х, який може впливати на зміну величини дисперсії залишків. Оскільки в табл. 7.3 дані про дохід упорядковані, то переходимо до наступного кроку.
Крок 2. Відкинемо c спостережень, які міститимуться в центрі векторів Х і Y, де 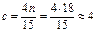 , і поділимо сукупність спостережень на дві частини, кожна з яких містить
, і поділимо сукупність спостережень на дві частини, кожна з яких містить 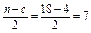 спостережень.
спостережень.
Крок 3. Побудуємо економетричну модель за першою сукупністю, яка включає спостереження від першого по сьомий місяць включно: 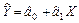 . Система нормальних рівнянь для визначення параметрів цієї моделі запишеться так:
. Система нормальних рівнянь для визначення параметрів цієї моделі запишеться так:
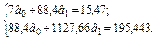
Звідси 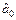 = 2, 1216;
= 2, 1216;
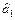 = 0, 007.
= 0, 007.
Економетрична модель має вигляд
I: 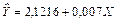 .
.
Крок 4. Побудуємо економетричну модель виду 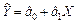 за другою сукупністю спостережень, починаючи від дванадцятого по вісімнадцятий місяць.
за другою сукупністю спостережень, починаючи від дванадцятого по вісімнадцятий місяць.
Система нормальних рівнянь для визначення параметрів цієї моделі запишеться так:
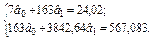
Звідси 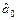 = – 0, 408;
= – 0, 408;
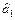 = 0, 165.
= 0, 165.
Економетрична модель має вигляд:
II: 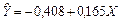
Крок 5. Знайдемо розрахункові значення залежної змінної моделі 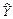 — величини заощадження за кожною з двох моделей і визначимо відхилення фактичних значень заощаджень від розрахункових.
— величини заощадження за кожною з двох моделей і визначимо відхилення фактичних значень заощаджень від розрахункових.
Таблиця 7.5 Таблиця 7.6
| Місяць | у |  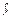
| u | u 2 | Місяць | y | 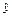
| u | u 2 | |
| 2, 36 | 2, 00 | 0, 36 | 0, 1296 | 2, 95 | 2, 99 | –0, 04 | 0, 0016 | |||
| 2, 20 | 2, 06 | 0, 14 | 0, 0196 | 2, 82 | 3, 09 | –0, 27 | 0, 0729 | |||
| 2, 08 | 2, 13 | –0, 05 | 0, 0025 | 3, 04 | 3, 21 | –0, 17 | 0, 0289 | |||
| 2, 20 | 2, 19 | 0, 01 | 0, 0001 | 3, 53 | 3, 37 | 0, 16 | 0, 0256 | |||
| 2, 10 | 2, 24 | –0, 14 | 0, 0196 | 3, 94 | 3, 56 | 0, 38 | 0, 1444 | |||
| 2, 12 | 2, 34 | –0, 22 | 0, 0484 | 3, 75 | 3, 68 | 0, 07 | 0, 0049 | |||
| 2, 41 | 2, 43 | –0, 02 | 0, 0004 | 3, 99 | 3, 83 | 0, 16 | 0, 0256 | |||
| Разом | 0, 2202 | Разом | 0, 3039 |
У табл.7.5 наведено результати обчислення суми квадратів залишків за першою моделлю S 1 = 0, 2202.
У табл.7.6 наведено обчислення суми квадратів залишків за другою моделлю S 2 = 0, 3039.
Крок 6. Обчислимо критерій R*, який наближено відповідає F -розподілу:
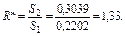
Порівняємо його значення з табличним значенням F -критерію при вибраному рівні довіри Р = 0, 99 і ступенях свободи g1 = 5 і g2 = 5. F табл = 11. Звідси R * < F табл, що свідчить про відсутність гетероскедастичності.
* Обидва терміни — гомоскедастичність і гетероскедастичність запропоновані російським вченим А.А.Чупровим (Див.: Основные проблемы теории корреляции. — 2-е изд. — М.: Госстатиздат, 1960, с. 39).