
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Список рекомендованої літератури
|
|
1. Управление автосервисом / Под общ. ред. Л. Б. Миротина. – М.: Издательство “Экзамен”, 2004. – 320 с.
5. Волгин В. В. Автомобильный дилер: практическое пособие по маркетингу и менеджменту сервиса и запасних частей. – М.: “Ось-89”, 1997. – 224 с.
3. Фастовцев Г. Ф. Организация технического обслуживания и ремонта легковых автомобилей. – М.: Транспорт, 1989. – 240 с.
4. Марков О. Д. Автосервіс: організація роботи з клієнтурою. – Київ: “Міжнародна агенція “BeeZone”, 2003. – 352 c.
5. Российская автотранспортная энциклопедия. Техническая эксплуатация, обслуживание и ремонт автотранспортних средств. – Т.3. – М.: РООИП – “За социальную защиту и справедливое налогообложение”, 2000. – 456 с.
6. Курніков І. П., Андрусенко С. І., Бортницький П. І. та ін. (2003) Технологічне проектування підприємств автосервісу. – К.: Видавництво “Іван Федоров”, 2003. - 262 с.
7. Напольский Г. М. Технологическое проектирование автотранспортных предприятий и станций технического обслуживания. – М.: Транспорт, 1993. – 272 с.
Додаток А Приклад вирішення практичного завдання
Фірма розглядає питання про будівництво станції технічного обслуговування (СТО) автомобілів. Складено кошторис видатків на будівництво станції різної потужності (з різною кількістю автомобілів, що обслуговуються, Nj), а також розраховано очікуваний прибуток Сij залежно від задоволення прогнозованого попиту li на запропоновані послуги СТО. Залежно від ухваленого рішення – проектної кількості автомобілів, що обслуговують за добу (проект СТО) Nj, та величини прогнозованого попиту на послуги СТО – побудована таблиця щорічних фінансових результатів (прибуток Cji, грошові одиниці).
Таблиця А.1 - Щорічні фінансові результати функціонування різних варіантів СТО
| Проект СТО Nj | Ступень задоволення попиту lj, % | |||||
| -120 | ||||||
| -160 | ||||||
| -210 | -30 | |||||
| -270 | -80 |
Вид та обсяг вихідної інформації дозволяють класифікувати середовище ухвалення рішення про будівництво СТО як не визначену. Множина її станів має кінцеве значення.
Стан зовнішнього середовища характеризується прогнозованою величиною задоволення попиту li з урахуванням
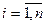 ,
,
де п – кількіст ь можливих станів середовища.
Всі можливі стани відомі. Невідомо тільки, який стан буде мати місце в умовах, коли планується реалізація прийнятого управлінського рішення. Будемо вважати, що безліч управлінських рішень (варіантів будівництва нової СТО) Nj має кінцеве значення й дорівнює т. Реалізація Nj варіанта за умов, коли зовнішнє середовище перебуває в li, стані, приводить до певного результату, який можна оцінити, увівши кількісну міру. У якості цієї міри у даному випадку служить прибуток від реалізації прийнятого варіанта СТО або ризик. Перетворимо вихідні дані в матрицю, рядки якої відповідають можливим варіантам потужності Nj, астовпці – ступеню задоволення попиту lj.
| l1 | l2 | … | li | … | ln | |
| N1 | C11 | C12 | … | C1i | … | C1n |
| N2 | C21 | C22 | … | C21 | … | C2n |
| … | … | … | … | … | … | |
| Nj | Cj1 | Cj2 | … | Cji | … | Cjn |
| … | … | … | … | … | … | |
| Nm | Cm1 | Cm2 | … | Cmi | … | Cmn |
Дана матриця є матрицею виграшів (у цьому випадку виграшем є прибуток Cji).
| l1 | l2 | l3 | l4 | l5 | l6 | |
| N1 | -120 | |||||
| N2 | -160 | |||||
| N3 | -210 | -30 | ||||
| N4 | -270 | -80 |
Безпосередній аналіз матриць виграшів || Cji || не дозволяє в загальному випадку ухвалити рішення щодо вибору оптимальної стратегії (варіанта будівництва), за винятком тривіального випадку, коли виграші при одній стратегії вищі, ніж при будь-який іншій для кожного стану середовища (елементи матриці виграшів у деякому рядку більше, ніж у будь-який іншій). Дані матриці, що складена не відповідають такому випадку, тому для ухвалення рішення в розглянутих умовах невизначеності скористаємося рекомендованими критеріями Лапласа, Вальда, Севіджа та Гурвица, які рекомендуються для таких випадків.
Критерій Лапласа.
Цей критерій враховує «принцип недостатньої підстави», відповідно до якого всі стани зовнішнього середовища lI 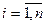 , вважаються рівноймовірними. Відповідно до цього принципу кожному стану lI ставиться ймовірність qi:
, вважаються рівноймовірними. Відповідно до цього принципу кожному стану lI ставиться ймовірність qi: 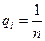
Для ухвалення рішення для кожного проекту Nj обчислюють середнє арифметичне значення одержуваного прибутку:
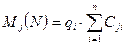
Вибираємо максимальне значення Mj(N), що буде відповідати оптимальному варіанту будівництва.
Результати розрахунків наведені в таблиці 1.2
Критерій Вальда.
Цей критерій враховує принцип найбільшої обережності, оскільки він ґрунтується на виборі найкращого з найгірших варіантів СТО Nj.
Оскільки у вихідній матриці за умовою завдання результат Сij – це виграш (прибуток), тоді під час вибору оптимальної стратегії використовується maxmin критерій. Для визначення оптимального варіанту будівництва СТО Nj у кожному рядку матриці результатів знаходимо найменший елемент min{ Сij }, а потім вибираємо варіант (рядок), якому будуть відповідати найбільші елементи із цих найменших елементів, тобто дія, що визначає результат, який дорівнює
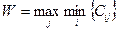
Результати розрахунків наведені в таблиці 1.2.
Таким чином, найкращим варіантом будівництва відповідно до maxmin критерія «кращим з гірших» буде Nj.
Мaxmin критерій Вальда іноді приводить до нелогічних висновків через свою надмірну обережність. Цей недолік виправляє критерій Севіджа.
Критерій Севіджа.
Використання даного критерію вимагає перетворення матриці «виграшів» || Cji || у матрицю ризиків || rji ||.
Ризик – різниця між результатом, який можна одержати, якщо знати дійсний стан зовнішнього середовища, і результатом, який маємо під час прийняття j-го варіанта будівництва.
rji визначає величину втрат особи, що приймає рішення. Отже, до rji можна застосовувати тільки minmax критерій. Критерій Севіджа рекомендує за умов невизначеності вибирати той варіант будівництва Nj, під час якого величина ризику приймає найменше значення у найнесприятливішій ситуації (коли ризик максимальний).
Елементи матриці ризиків пов'язані з елементами матриці виграшів (прибутків) наступним чином:
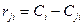 ,
,
де 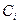 – максимальний елемент в i-м стовпці матриці || Cji ||
– максимальний елемент в i-м стовпці матриці || Cji ||
rji – це різниця між найкращим значенням у стовпці i та зна-
ченнями Cjiз урахуванням того ж i.
| l1 | l2 | l3 | l4 | l5 | l6 | |
| N1 | ||||||
| N2 | ||||||
| N3 | ||||||
| N4 |
Незалежно від того, чи є Cji, прибутком або витратами, rji в обох випадках визначає величину втрат особи, що приймає рішення. Отже, можна застосовувати до rjiтільки minmax критерій. В умовах невизначеності Критерій Севіджа рекомендує вибирати той варіант Cji, при якому величина ризику приймає найменше значення в найнесприятливішій ситуації (коли ризик максимальний).
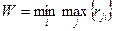
Застосування критерію Севіджа дозволяє будь-якими шляхами уникнути великого ризику при виборі стратегії, тобто, уникнути більшого програшу (втрат).
Таблиця А.2 - Результати визначення критеріїв Лапласа, Вальда та Севіджа
| Критерій Лапласа | Критерій Вальда | Критерій Севіджа | ||||
| Імовірність вибору варіанту qi | Середнє значення доходу | Найкращій варіант Mi(N) | Мin значення прибутку, min{Сji} | Найкращій варіант | Max значення ризику, max {rji} | Найкращій варіант, minmax {rji} |
| 232, 5 | -120 | -120 | ||||
| 0, 25 | 301, 25 | -160 | ||||
| -210 | ||||||
| -270 |
Критерій Гурвиця.
Даний критерійзаснований на наступних двох припущеннях: зовнішнє середовище може перебувати в самому невигідному стані з імовірністю (1-a) і в самому вигідному стані з імовірністю a, де a - коефіцієнт довіри. Для результату у вигляді прибутку критерій Гурвиця записується як:
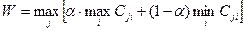
Таблиця А.3 - Результати визначення критерію Гурвиця
| Критерій Гурвиця | ||||
| Max значення доходу, max{Cji} | Min значення доходу, min{Cji} | Коефіцієнт довіри, a | W= a max{Cji}+(1- a) min{Cji} | Найкращій варіант, max Wj |
| -120 | ||||
| -160 | 0, 5 | |||
| -210 | ||||
| -270 |