Теоретические сведения. Цель работы– освоить навыки приближенного нахождения корней алгебраических трансцендентных уравненийметодом итераций в различных средах программирования.

Лабораторная работа № 16

ОПРЕДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

МЕТОДОМ ИТЕРАЦИЙ

Цель работы – освоить навыки приближенного нахождения корней алгебраических трансцендентных уравненийметодом итераций в различных средах программирования.

Постановка задачи

1. Используя метод итераций, вычислить с заданной точностью (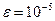) действительные корни заданного алгебраического уравнения .

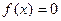2. Решить задачу в различных средах: Fortran, MS Excel и MathCad.

Теоретические сведения

Пусть дано уравнение

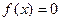, (1)

где 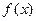- непрерывная функция.

Требуется вычислить действительный корень уравнения, находящийся на отрезке .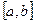

Приводим заданное уравнение 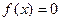к виду

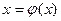, (2)

где 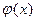- некоторая непрерывная на отрезке функция.

Выбираем произвольное 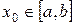и подставляем его в правую часть равенства (2):

.

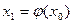Аналогично получаем

;

;

…

.

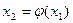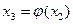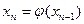Доказано, что если последовательность 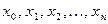сходится, то её пределом является корень уравнения (2), а значит, и корень уравнения (1), так как уравнения (1) и (2) равносильны.

Для сходимости итерационного процесса исходное уравнение 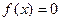достаточно привести к виду 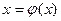так, чтобы выполнялось условие

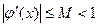(3)

при .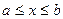

Это достигается различными способами. Например, уравнение 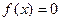заменяем равносильным 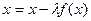. В этом случае 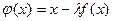. Параметр 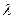выбираем так, чтобы 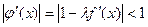при 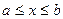. Уравнение 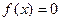можно преобразовать к виду 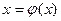разными способами, лишь бы функция 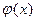удовлетворяла условию (3).

Пример 1. Привести уравнение 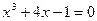к виду, пригодному для применения метода итераций. Единственный действительный корень заданного уравнения находится на отрезке 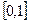, так как , .

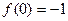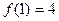Приводим исходное уравнение к виду

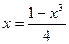. (4)

В этом случае 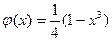. Тогда 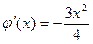, 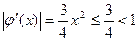при .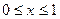

Таким образом, достаточное условие сходимости итерационного процесса выполняется.

Метод итераций применим для решения уравнения (4). Выбираем произвольное 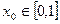, например, 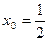. Тогда

.

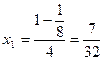Аналогично определяются последующие приближения.

Пример 2. Привести уравнение 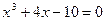к виду, пригодному для применения метода итераций.

Единственный корень заданного уравнения находится на отрезке 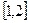. Рассмотренный в примере 1 способ в данном случае неприменим, так как при этом не удовлетворяется достаточное условие сходимости итерационного процесса. Заменяем исходное уравнение равносильным:

.

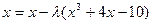В этом случае

; .

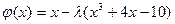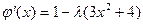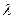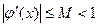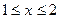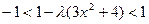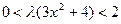Параметр находим из условия при , т.е. или при 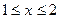. Отсюда .

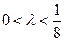Полагаем, например, 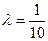. Исходное уравнение преобразуем к виду

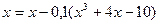, (5)

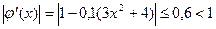причем при .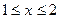

Методом итерации можно решать уравнение (5).

Выбираем произвольное 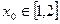. Пусть 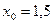. Используя уравнение (5), вычисляем 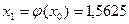. Подставляя 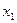в правую часть равенства (5), получаем 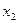и т.д. Вычисления производим до тех пор, пока выполнится неравенство .

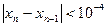Типовый вариант

Вычислить корни уравнения 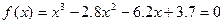методом итераций

с точностью e =10^-5 на предварительно найденном интервале изоляции [a, b].

Реализация типового варианта