Тема: ИЗГИБ

Раздел 2 Сопротивление материалов

Задание №3

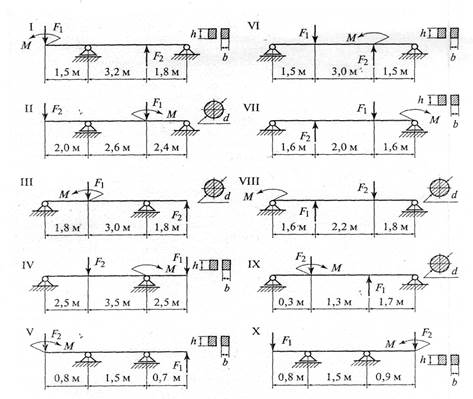
ЗАДАНИЕ. Для заданной двухопорной балки определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Подобрать из условия прочности на изгиб размеры поперечного сечения прямоугольника или круга, приняв для прямоугольника h= 2b. Считать [σ _и]= 150 МПа.

Данные для различных вариантов указаны в табл. 1.

Таблица 1

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Изгиб- это такой вид нагружения балки, при котором в ее поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы; такой изгиб называют поперечным. Если поперечные силы не возникают, изгиб называют чистым.

Изгибающий момент в произвольном сечении равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть балки:

М_и=Ʃ М_о(F_i).

Поперечная сила Q равна алгебраической сумме проекций внешних сил, действующих на отсеченную часть балки:

Q=Ʃ F_iy.

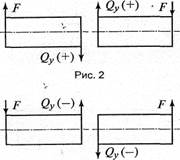Рис. 3 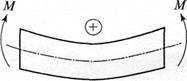Рис. 4 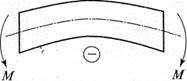Рис. 5

Правило знаков для поперечных сил: поперечная сила считается положительной, если внешние силы поднимают левый конец балки или опускают правый конец (рис. 2), и отрицательной, если внешние силы опускают левый конец балки или поднимают правый конец (рис. 3). Правило знаков для изгибающих моментов: изгибающий момент считается положительным, если внешние силы, действующие на левый конец балки, поворачивают его по часовой стрелке, а действующие на правый - против часовой стрелки (рис. 4), и отрицательным, если внешние силы поворачивают левый конец балки против часовой стрелки, а правый - по часовой (рис. 5). Для балок, имеющих много участков нагружения, эпюры изгибающих моментов Ми строятся по характерным точкам, т.е. точкам, в которых приложены внешние силы и моменты. Для определения опорных реакций балки используются равновесия: Ʃ Fix = 0 Ʃ Fiy = 0 Ʃ Mo(Fi) = 0

Пример. Для заданной двухопорной балки (рис. 6, а) определить реакции опор, построить эпюры поперечных сил и изгибающих моментов, определить размеры поперечного сечения (h, b, d) в форме прямоугольника и круга, приняв для прямоугольника h/b=1, 5. Считать [σ _и] = 160 МПа. Дано: F₁ = 18 кН, F₂ =30 кН, M₁=20 кН·м, М₂= 10 кН·м.

Решение. 1. Строим расчетно-графическую схему (рис. 6, б).

2. Определяем опорные реакции балки

R_Bx = 0, R_By = 10 кН, R_D = 22 кН.

Проверка: Ʃ F_iy = 0

-F₁+ R_By+F₂-R_D = 0

-18+10+30-22 = 0

-40+40 = 0

Условие равновесия статики выполняется, следовательно, реакции опор балки найдены правильно:

R_By=0, R_By = 10 Кн, R_D = 22 кН.

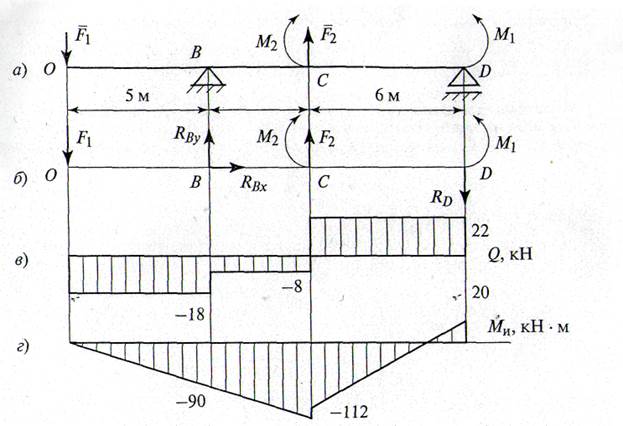
Рис. 6

3. Определяем поперечные силы Q в характерных точках: O, B, C, D и строим эпюру слева направо (рис. 6, в):

Q_O = -F₁ = -18 кН

Q_{B слева} = -F₁ = -18 кН

Q_{B справа} = -F₁ + R_By = -18 + 10 - -8 кН

Q_{C слева} = -F₁ + R_By= -18 + 10 = -8 кН

Q_{C справа} = -F₁ + R_By + F₂ = -18 + 10 + 30 = 22 кН

Q_{D слева} = -F₁ + R_By + F₂ = -18 + 10 + 30 = 22 кН

4. Вычисляем изгибающие моменты в тех же характерных точках O, B, C, D и строим их эпюру (рис. 6, г):

М_{и О} = 0,

М_{и B} = -F₁ OB = -18 · 5 = -90 кН · м,

М_{и С слева} = -F₁ OC + R_By BC = -18 · 9 + 10 · 4 = -122 кН · м,

M_{и С справа} = - F₁ OC + R_By BC + M₂ = -18 · 9 + 10 · 4 + 10 = -112 кН · м,

М_{и D} = -F₁ OD + R_By BD + M₂ + F₂ CD = -18 · 15 + 10 · 10 + 10 + 30 · 6 = 20 кН.

5. Вычисляем размеры сечения данной балки по двум вариантам:

а) сечение – прямоугольник с заданным соотношением сторон;

б) сечение – круг.

Вычисляем размеры прямоугольного сечения из условия прочности на изгиб

σ _и = .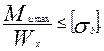

Максимальный изгибающий момент берется в точке С слева М_{и max} = 122 кН · м.

.

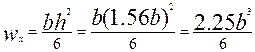Так как h/b =1.5, то h = 1, 5b.

Тогда

.

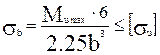Отсюда

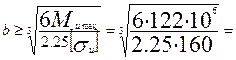127 мм

(1 кН·м = 10⁶ Н · мм).

Так как b = 127 мм, то

H = 1.5b = 1.5 · 127 = 190.5 мм.

Вычисляем размер круглого сечения из условия прочности на изгиб

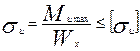
Так как для круга 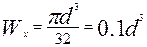, то

.

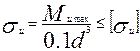Отсюда находим диаметр сечения:

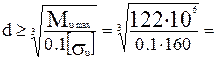195 мм.

Ответ: b = 127 мм; h = 190, 5 мм; d = 195 мм.