Аппроксимация данных методом наименьших квадратов

Расчетно-графическая работа №2

ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Цель – закрепить навыки разработки графического приложения Fortran для решения простейших инженерных задач; освоить приемы работы с выводом графика нескольких функций; изучить основы применения численной аппроксимации таблично заданных функций методом наименьших квадратов и решения систем линейных алгебраических уравнений методом исключений Гаусса.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Аппроксимация данных методом наименьших квадратов

Пусть в результате эксперимента получена таблица значений функции:

Требуется аппроксимировать эту функцию многочленом степени m (m< n):

.

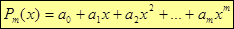Согласно методу наименьших квадратов (МНК) ищем значения параметров 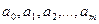, при которых сумма квадратов

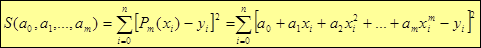
принимает минимальное значение.

С учетом необходимых условий существования экстремума функции нескольких переменных получаем систему уравнений для определения неизвестных :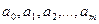

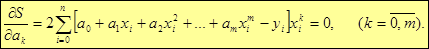
Доказано, что система уравнений имеет единственное решение, при котором 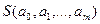принимает минимальное значение.

Рассмотрим частные случаи.

Случай 1. Пусть 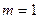, т.е. функцию аппроксимируем многочленом первой степени:

.

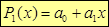Система уравнений для вычисления параметров 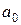, 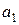имеет следующий вид:

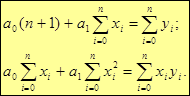
Решив систему, можем записать требуемый многочлен .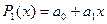

Случай 2. Пусть 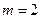, т.е. функцию аппроксимируем многочленом второй степени:

.

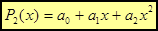Система уравнений для определения параметров 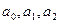имеет следующий вид:

Решив систему, можно записать многочлен 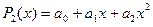.