Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение системы линейных алгебраических уравнений методом Гаусса
|
|
Представим исходную систему линейных алгебраическихуравнений (СЛАУ) в виде
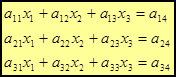 (1)
(1)
 Делим первое уравнение системы (1) на
Делим первое уравнение системы (1) на  . В результате получим уравнение
. В результате получим уравнение
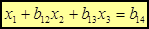 , (2)
, (2)
где 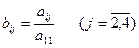 .
.
Из второго уравнения системы (1) вычитаем уравнение (2), умноженное на 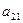 , а из третьего уравнения системы (1) – уравнение (2), умноженное на
, а из третьего уравнения системы (1) – уравнение (2), умноженное на 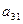 . Получаем систему
. Получаем систему
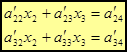 (3)
(3)
где 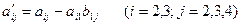 .
.
 Делим первое уравнение системы (3) на
Делим первое уравнение системы (3) на 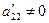 . В результате получим уравнение
. В результате получим уравнение
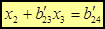 , (4)
, (4)
где 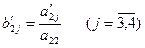 .
.
Умножая уравнение (4) на 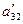 и вычитая его из второго уравнения системы (3), получаем:
и вычитая его из второго уравнения системы (3), получаем:
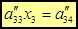 , (5)
, (5)
где 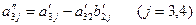 .
.
Наконец, разделив уравнение (5) на 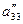 , получим:
, получим:
 , (6)
, (6)
Используя уравнения (4) и (2), находим последовательно 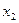 и
и 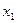 .
.
ВАРИАНТ ЗАДАНИЯ
| № варианта | Исходные данные | |||||||
| x | -1 | |||||||
| y | 3, 1 | 2, 8 | 2, 4 | 2, 1 | 1, 9 | 2, 2 | 2, 6 |
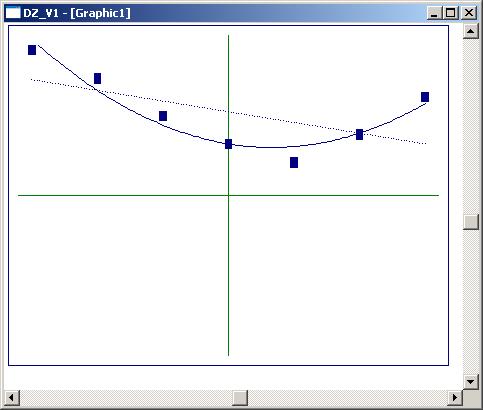
Требуется методом наименьших квадратов найти многочлены первой и второй степеней, аппроксимирующие заданную функцию.
ВЫПОЛНЕНИЕ ВАРИАНТА
1. Текстовый файл DZ_V1.txt.
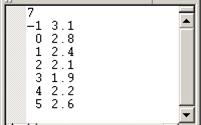
2. Результаты аппроксимации таблично заданной функции с помощью метода наименьших квадратов. Кривая параболы должна более качественно и точнее отвечать процессу, представленному таблично заданной функцией.