
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решетчатые фильтры для стационарных случайных процессов
|
|
Построение АР модели или синтез АР фильтра требуют вычисления коэффициентов АР. Для этого необходимо обращать корреляционную матрицу, а эта операция, как правило, сопряжена с большим объемом вычислений. Поиски эффективных алгоритмов вычисления коэффициентов АР привели к синтезу решетчатых структур. Решетчатые структуры могут быть реализованы в виде решетчатых фильтров (РФ). Параметрами РФ являются коэффициенты отражения и число звеньев фильтра. Коэффициенты отражения однозначно связаны с параметрами АР и определяются, в конечном счете, корреляционной функцией случайного процесса. Число звеньев РФ равно порядку АР модели РФ, также как и АР фильтры, являются фильтрами предсказания, минимизирующими дисперсию ошибки предсказания.
Несмотря на то, что АР фильтры и РФ математически эквивалентны, между ними существует ряд различий, существенных с практической точки зрения. При цифровой реализации фильтров особое значение играет шум округления. Его появление связано с тем, что значения величин приходится представлять конечным числом разрядов. Как показывает опыт, в этом отношении РФ более эффективны. Объясняется это тем, что ошибки округления i-1-го звена в РФ частично компенсируются в i-м звене РФ, чего нет в АР фильтрах. Другим существенным свойством цифровых фильтров является их чувствительность к квантованной форме представления параметров фильтра. Поэтому, естественно, возникает вопрос: насколько сильно зависят характеристики фильтра от отклонения величин параметров. Доказано, что РФ менее чувствительны к погрешностям квантования параметров по сравнению с фильтрами прямой реализации. При синтезе РФ, состоящего из p звеньев, используются те же коэффициенты отражения, что и у p-1-звенного фильтра. В АР фильтре же при увеличении числа звеньев фильтра, приходится заново пересчитывать все коэффициенты АР фильтра. Следовательно, использование РФ для обработки случайных сигналов имеет ряд преимуществ перед АР фильтрами.
2.3 Синтез решетчатого фильтра
Несмотря на близость РФ к АР фильтрам, использование РФ требует введения новых понятий и соотношений, на основе которых выводится структура РФ. Прежде всего, необходимо остановиться на выводе рекуррентных соотношений, которые носят название алгоритма Левинсона-Дарбина. Алгоритм позволяет вычислять коэффициенты отражения РФ по найденным коэффициентам АР модели сигнала 1- р порядков.
По аналогии с фильтром прямого предсказания для сигнала, описываемого моделью АР р-го порядка, можно ввести фильтр обратного предсказания, описываемый выражением
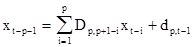 , (2.15)
, (2.15)
где 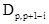 - коэффициенты фильтра обратного предсказания, состоящего из р звеньев, определяемые моделью АР, введенной во второй главе,
- коэффициенты фильтра обратного предсказания, состоящего из р звеньев, определяемые моделью АР, введенной во второй главе, 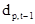 - ошибка обратного предсказания на выходе р-го звена фильтра. Уравнение описывает регрессию значения случайного процесса хt-p-1 на последующие хt-p, хt-1-p,..., хt-1. Значения коэффициентов фильтра обратного предсказания находятся с помощью системы уравнений, аналогичной системе уравнений Юла-Уокера. Объединяя уравнения (2.4а) и (2.4б), можно представить обобщенные уравнения Юла-Уокера в матричном виде
- ошибка обратного предсказания на выходе р-го звена фильтра. Уравнение описывает регрессию значения случайного процесса хt-p-1 на последующие хt-p, хt-1-p,..., хt-1. Значения коэффициентов фильтра обратного предсказания находятся с помощью системы уравнений, аналогичной системе уравнений Юла-Уокера. Объединяя уравнения (2.4а) и (2.4б), можно представить обобщенные уравнения Юла-Уокера в матричном виде
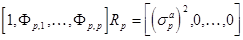 , (2.16)
, (2.16)
где 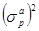 -квадрат СКО, равный дисперсии ошибки прямого предсказания, Rp - корреляционная матрица (p+1) порядка
-квадрат СКО, равный дисперсии ошибки прямого предсказания, Rp - корреляционная матрица (p+1) порядка
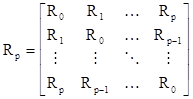 . (2.17)
. (2.17)
Чтобы не выходить за рамки общепринятых в теории решетчатых фильтров обозначений (например [16, 17]), в дальнейшем изложении будет использоваться замена 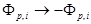 и
и 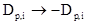 .
.
Умножив левую и правую части уравнения на 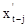 ; j=1, p+1 и усреднив, легко получить уравнение Юла-Уокера для фильтра обратного предсказания, аналогичное (2.16)
; j=1, p+1 и усреднив, легко получить уравнение Юла-Уокера для фильтра обратного предсказания, аналогичное (2.16)
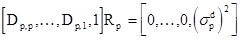 , (2.18)
, (2.18)
где 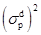 - дисперсия ошибки обратного предсказания на выходе p-го звена фильтра обратного предсказания.
- дисперсия ошибки обратного предсказания на выходе p-го звена фильтра обратного предсказания.
Объединив матричные уравнения (2.16) и (2.18) можно записать более общее уравнение
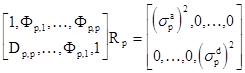 . (2.19)
. (2.19)
Очевидно, что для (р+1)- звенного фильтра должно так же выполняться соотношение типа
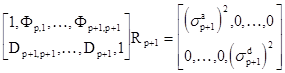 . (2.20)
. (2.20)
Но, как показано в [5, 7], от матричного уравнения (2.19) можно перейти к матричному уравнению (2.20) лишь в том случае, если коэффициенты фильтров прямого и обратного предсказания p-го порядка связаны с коэффициентами фильтра (p+1)-го порядка следующим образом
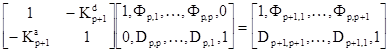 , (2.21)
, (2.21)
где 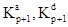 - некоторые, так называемые, коэффициенты отражения. Умножив справа левую и правую часть матричного уравнения (2.21) на корреляционную матрицу Rp+1, можно показать, что коэффициенты отражения удовлетворяют соотношениям
- некоторые, так называемые, коэффициенты отражения. Умножив справа левую и правую часть матричного уравнения (2.21) на корреляционную матрицу Rp+1, можно показать, что коэффициенты отражения удовлетворяют соотношениям
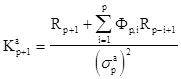 , (2.22а)
, (2.22а)
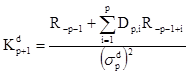 . (2.22б)
. (2.22б)
Величины, входящие в соотношения (2.22а) и (2.22б), описываемые выражениями
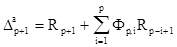 , (2.23а)
, (2.23а)
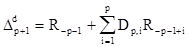 , (2.23б)
, (2.23б)
как будет показано ниже, интерпретируются как взаимная корреляция ошибок прямого и обратного предсказания при единичной задержке. Для скалярного случая справедливы равенства
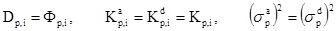 . (2.24)
. (2.24)
Используя соотношения (2.15), (2.22а), (2.22б) и учитывая (2.24), алгоритм Левинсона-Дарбина, позволяющий вычислять коэффициенты АР по коэффициентам отражения, можно представить в виде
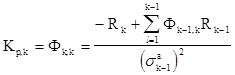 , k=2, p, (2.25)
, k=2, p, (2.25)
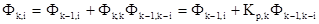 , (2.26)
, (2.26)
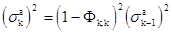 , (2.27)
, (2.27)
с инициацией
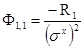 ,
, 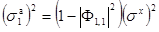 . (2.28)
. (2.28)
Найденный алгоритм Левинсона-Дарбина позволяет получить структуру РФ. Формулы (2.29) и (2.30) дают выражение
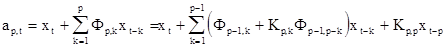 , (2.29)
, (2.29)
которое с помощью (2.29) приводится к виду
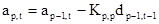 . (2.30)
. (2.30)
Аналогично можно найти выражение для ошибки обратного предсказания
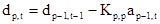 . (2.31)
. (2.31)
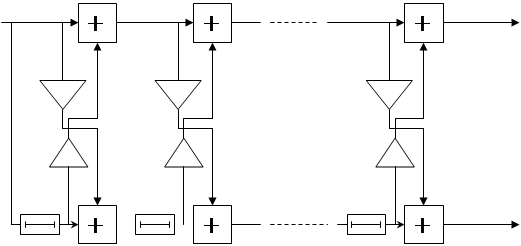
Полученные выражения (2.30) и (2.31) дают возможность представить структуру РФ в виде, изображенном на рисунке 2.1.

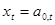
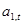
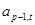
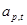
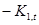
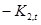
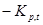
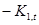
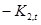
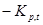
 |
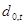
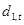
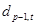
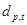
Рисунок 2.1 -Обеляющий РФ.
При поступлении сигнала на вход фильтра на выходе каждого звена фильтра появятся ошибки предсказания вперед и назад. Как видно из рисунка 2.1 ошибки предсказания вперед и назад связаны друг с другом соотношениями (2.30) и (2.31).
Как можно показать, используя соотношение (2.31), решение задачи минимизации дисперсии ошибки предсказания 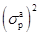 относительно коэффициента отражения Кp дает следующее выражение для коэффициента отражения
относительно коэффициента отражения Кp дает следующее выражение для коэффициента отражения
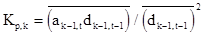 . (2.32)
. (2.32)
К этому же соотношению можно придти путем несложных преобразований выражений (2.30) и (2.31). Таким образом, РФ, коэффициенты отражения которого определяются алгоритмом Левинсона-Дарбина, минимизирует дисперсию ошибки предсказания. Выражение (2.32) дает удобную оценку коэффициентов отражения РФ, позволяющее обновлять их при адаптации фильтра.
Из рисунка 2.1 видно, что текущий отсчет случайного процесса можно представить в виде
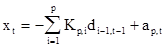 ,
, 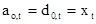 , (2.33)
, (2.33)
т.е. взвешенным суммированием ошибок обратного предсказания в предшествующий момент времени с коэффициентами веса, равными коэффициентам отражения. Случайная величина хt, представленная в виде ряда, полностью определяется коэффициентами разложения, роль которых играют коэффициенты отражения. Таким образом, коэффициенты отражения полностью характеризуют случайный процесс в рамках модели АР. Это свойство коэффициентов отражения РФ позволяет использовать их в качестве информативного признака при распознавании.
2.4 Примеры обработки стационарных случайных процессов с помощью решетчатых фильтров
Неадаптивные РФ используются для обработки стационарных коррелированных процессов. Примерами задач, решаемых с помощью таких фильтров, может служить применение РФ для подавления или обеления стационарных коррелированных помех, измерение некоторых параметров сигнала, кодировании и генерации случайных процессов и синтез речи, создание эффективных вычислительных алгоритмов и т.д.
Эффективность обработки сигналов РФ определяется точностью АР моделирования этих сигналов, достоверностью используемых оценок параметров фильтра и сигнала, скоростью и объемом необходимых вычислений. Наиболее простым способом проверки соответствия параметров РФ характеристикам обрабатываемых сигналов может служить мера близости сигнала на выходе РФ к белому шуму. Это следует из принципа построения РФ по минимуму дисперсии ошибки предсказания.
1.2.2. Генерация случайных процессов на основе фильтра с решетчатой структурой
Дальнейшее развитие теории в области предсказания временных рядов на основе модели АР привело к созданию так называемых фильтров на решетчатых структурах. Реализация решетчатых структур в виде решетчатых фильтров (РФ) предсказания по методу наименьших квадратов выявила целый ряд достоинств РФ. Особенно это касается адаптивныхметодов обработки случайных процессов. В стандарте GSM осуществляется адаптивная блочная обработка речи на основе фильтров предсказания с решетчатой структурой. Блочная адаптивная обработка процессов отличается от пошаговой тем, что параметры фильтра пересчитываются не с получением каждого нового отсчета данных, а по последовательным блокам данных. Параметры речи, а также процесс на выходе адаптивного РФ сформированные кодером на передающем сотовом телефоне, покадрово передаются через базовую станцию на приемник сотового телефона корреспондента. Декодер сотового телефона по принятым данным восстанавливает речевой сигнал. Для генерации речи применяется формирователь на базе РФ с обратной связью. Структура такого генератора приведена на рис. 2.

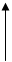






































|







|
|
|
|
|
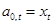
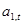
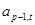

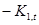
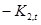
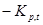
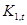
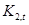
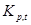
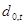
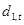
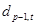
Рисунок 2.- Генератор коррелированного случайногопроцесса на
решетчатом фильтре с обратной связью.
РФ с прямым прохождением сигнала и РФ с обратной связью, имеющие одинаковые коэффициенты отражения, выполняют инверсные операции над входным сигналом. Если на вход РФ с прямым прохождением сигнала подается коррелированный случайный процесс, т. е. 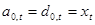 , то на выходе получаем ошибку предсказания типа белого шума
, то на выходе получаем ошибку предсказания типа белого шума 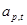 . В случае же когда на вход РФ с обратной связью подается случайный процесс типа белого шума, т. е.
. В случае же когда на вход РФ с обратной связью подается случайный процесс типа белого шума, т. е. 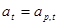 , то на выходе формируется коррелированный случайный процесс, т. е.
, то на выходе формируется коррелированный случайный процесс, т. е. 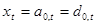 .
.
Работа генератора с кратковременным предсказанием на РФ описывается системой двух уравнений
 , (7а)
, (7а)
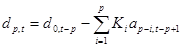 , (7б)
, (7б)
где 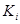 - коэффициенты отражения РФ;
- коэффициенты отражения РФ;  - число звеньев РФ;
- число звеньев РФ; 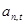 и
и 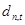 - ошибки прямого и обратного предсказания в
- ошибки прямого и обратного предсказания в 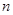 -м звене РФ в момент времени
-м звене РФ в момент времени 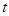 .
.
Применение для кодирования речи коэффициентов отражения РФ, которые являются также коэффициентами частичной корреляции случайного процесса, являются более предпочтительными, по сравнению с коэффициентами АР по следующим причинам:
- гарантируется стабильность работы генератора на РФ, т. к. согласно (8) и (10) 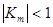 , а это является необходимым условием, чтобы передаточная функция была минимально фазовой функцией и ее полюсы находились внутри единичного круга на комплексной плоскости;
, а это является необходимым условием, чтобы передаточная функция была минимально фазовой функцией и ее полюсы находились внутри единичного круга на комплексной плоскости;
- коэффициенты 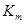 нечувствительны к ошибкам квантования;
нечувствительны к ошибкам квантования;
- при переходе от  -звенного к
-звенного к 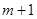 -звенному фильтру, значения
-звенному фильтру, значения 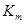 не пересчитываются, в то время как коэффициенты АР нужно пересчитывать заново;
не пересчитываются, в то время как коэффициенты АР нужно пересчитывать заново;
- коэффициенты отражения анализирующего и синтезирующего фильтров совпадают, что, впрочем, характерно и для коэффициентов АР.
В стандарте GSM в качестве порождающего процесса  , который подается на вход синтезатора речи, используют ошибки предсказания анализирующего РФ, пропущенные через НЧ фильтр, с частотой среза 3-4 кГц. Хотя такой способ возбуждения требует существенного увеличения скорости передачи до
, который подается на вход синтезатора речи, используют ошибки предсказания анализирующего РФ, пропущенные через НЧ фильтр, с частотой среза 3-4 кГц. Хотя такой способ возбуждения требует существенного увеличения скорости передачи до
9.4 кбит/с, качество восстановленного в декодере сигнала речи соответствует качеству передаваемой речи в цифровых каналах связи ISDN и превосходит качество речи в аналоговых радиотелефонных системах.
Можно показать, что передаточные функции анализирующего и синтезирующего РФ также описываются выражениями () и () соответственно.
Высокое качество передачи речи в стандарте GSM достигается не только учетом корреляции между соседними дискретизированного речевого сигнала, но и учетом тонкой структуры речевого сигнала – корреляции между отсчетами в соседних периодах основного тона. С этой целью используются предикторы с кратковременным и долговременным предсказанием соответственно. Синтезатор речи с кратковременным предсказанием описывается системой уравнений () и показан на рис. 2.
Выражение для долговременного предсказания в стандарте GSM определяется следующим образом
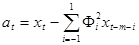 , (11)
, (11)
где  - число отсчетов в периоде основного тона.
- число отсчетов в периоде основного тона.
Тогда передаточная функция анализирующего фильтра может быть представлена в виде
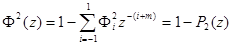 . (12)
. (12)
Передаточная функция синтезирующего фильтра описывается выражением, аналогичным ()
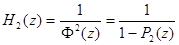 . (13)
. (13)
Систему уравнений описывающую синтезирующий РФ с долговременным предсказанием можно получить из ()
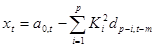 , (14)
, (14)
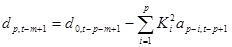 . (15)
. (15)