Теоретико-игровой подход в условиях конфликта Описание игры.

.

Пусть определено разбиение всего множества угроз безопасности на обобщенные угрозы, т.е. задано множество обобщенных угроз таких, что все угрозы безопасности, относимые к одной обобщенной угрозе, сходны по оказываемому на систему воздействию

Пусть; для каждой пары «уязвимость - обобщенная угроза» могут быть получены численные оценки потерь в результате реализации данной угрозы.

В этом случае предлагается использовать теоретико-игровые модели

в классе конечных игр двух игроков «защитника» и «нарушителя». Необходимо отметить, что в данной игре действиями «стороны У» моделируются как преднамеренные воздействия на систему, так и случайные события, которые могут привести к нежелательным последствиям. Выбор конечных теоретико-игровых моделей, реализующих принцип гарантированного результата определяется следующими характерными особенностями исследуемой задачи:

· наличие конфликта интересов «защитника» и «нарушителя»;

· присутствие фактора неопределенности;

· отсутствие достоверной статистической информации о действии нежелательных факторов;

· конечное множество обобщенных угроз;

· результаты действия стороны У; или случайных факторов можно оценить вещественным числом интерпретируемым как выигрыш одной из сторон.

Для построения игры необходимо определить стратегии игроков и функцию выигрыша. Пусть игрок I - «защитник», игрок II -«нарушитель» (источник угроз). Стратегии игрока I заключаются в выборе одного из вариантов системы противодействия угрозам или отказе от каких-либо действий. Стратегии игрока II - реализация одной из множества обобщенных угроз или бездействие.

Допустим, что действия каждого из игроков являются однократными или могут быть сведены к некоторому суммарному однократному воздействию на систему. Это допущение позволяет использовать одношаговые игровые модели.

Рассмотрим антагонистические конечные одношаговые игры. В них значение выигрыша «защитника» равно по модулю и противоположно по знаку значению выигрыша «нарушителя».

Обозначим множество вариантов з структуры системы противодействия 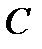. Текущее или начальное состояние системы противодействия можно описать в виде варианта 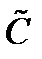, характеризуемого тем, что затраты на его осуществление равны 0. Тогда стратегия «защитника» (игрока I) будет заключаться в реализации одного из вариантов из множества .

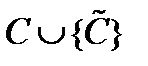Далее рассмотрим построение множества стратегий «нарушителя» (игрок У). Оно формируется на базе множества 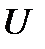- множества обобщенных угроз, дополненного стратегией 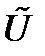, обозначающей бездействие нарушителя. В итоге множество стратегий игрока II будет равно 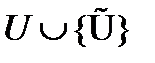. Антагонистическая игра задается следующей тройкой

,

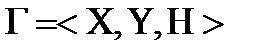где: 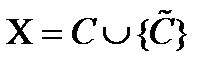- множество стратегий защитника: (сторонаХ) (сторона 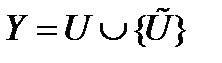множество стратегий нарушителя:

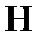- матрица выигрышей.

Пусть мощности множеств стратегий игроков равны: |Х|=m, |У|=n.

Представим матрицу выигрышей в следующем виде:

,

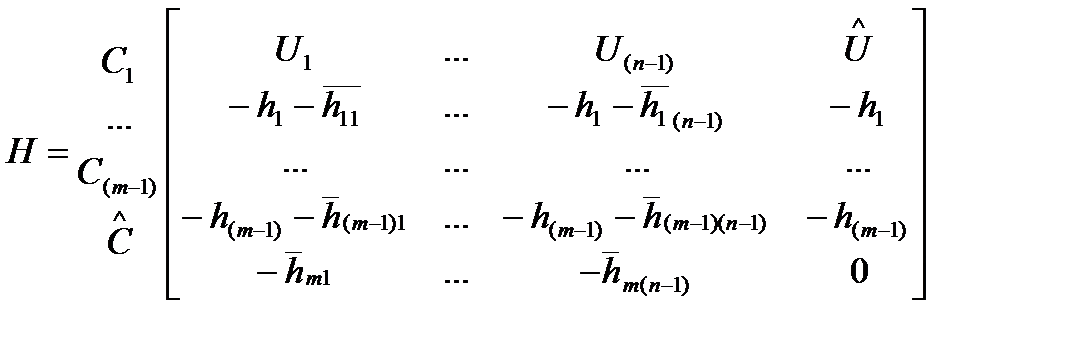где перед началом строк и столбцов указаны соответствующие элементы множеств X и У. В этой матрице использованы обозначения: 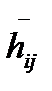- оценка потерь от реализации нарушителем j-й обобщенной угрозы, когда реализован i-й вариант системы противодействия; 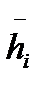размер величины затрат на реализацию i-го варианта исследуемой системы.

Оценки потерь 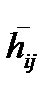могут быть получены по результатам анализа рисков (как правило, для их получения используется методы экспертных оценок). Если известен закон распределения вероятности появления случайных событий, создающих угрозу безопасности, то 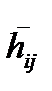математическое ожидание потерь.

В том случае, когда «нарушитель» ничего не предпринимает 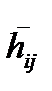=0 (последний столбец матрицы Н).

Затраты 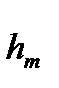на реализацию «защитником» последней стратегии (отказ от проведения дополнительных мероприятий по защите) также принимаются равными нулю.

Обе составляющие элемента матрицы Н взяты со знаком минус, т.к для игрока I («Х») - это отрицательный выигрыш (потери).

Построенная антагонистическая игра отражает ситуацию наиболее пессимистичного прогноза, когда реальные возможности и цели нарушителя неизвестны, и считается, что он всемогущ и его цель - нанести максимальный вред. Если можно достоверно определить возможности «нарушителя» и ценность для него результатов ЭМА, то возможно использование биматричной игровой модели. Биматричная игра задается следующей «четверкой»:

где Xи У - множества стратегий игроков Iи II, Н - матрица выигрышей защитника; Н₂ - матрица выигрышей нарушителя, которая формируется следующим образом:

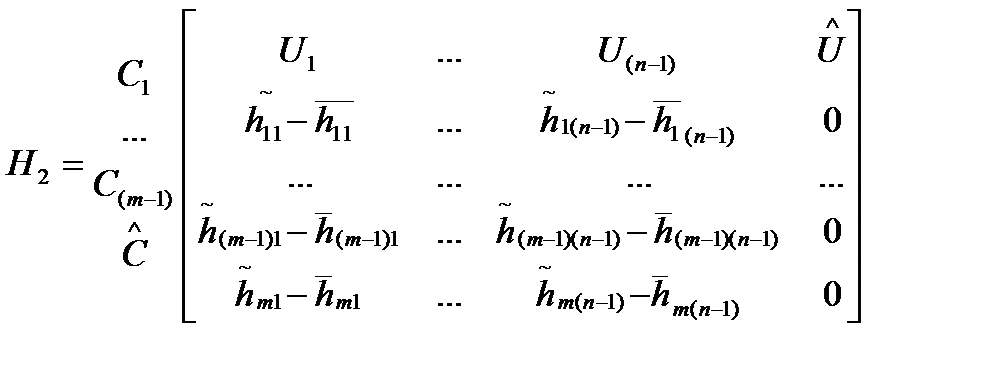
Где 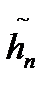- оценка выигрыша «нарушителя» от реализации j-й обобщенной угрозы в отношении i-го варианта системы противодействияобеспечения ЭМБ ; 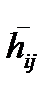- оценка затрат «нарушителя» на реализацию этой угрозы.

Для обобщенных угроз, источниками которых являются случайные события (например, отказ оборудования), значение 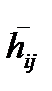принимается равным нулю, а величину 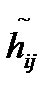предлагаетсявзять равной по модулю и обратной по значению, соответствующему элементу матрицы выигрышей игрока I. Нули в последнем столбце матрицы Н₂ соответствуют ситуации, когда «нарушитель» ничего не предпринимает.

По сравнению с антагонистической игровой моделью, биматричная модель отражает менее пессимистичный прогноз, основанный на наличии дополнительных знаний о «нарушителе». Соответственно, могут оказаться отличными от предыдущей модели и оптимальные стратегии.