
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выбор оптимальной стратегии
|
|
Рассмотренные теоретики игровые модели реализации политики безопасности относятся к классу «игр против природы». Играми против природы «называют модели принятия решения индивидом, когда функция выигрыша ему неизвестна, а точнее, известно лишь, что функция выигрыша " выбирается природой" из некоторого фиксированного множества. При этом неизвестны вероятности, с которыми выбирается та или иная функция». Задачей игрока I («защитника») является расстановка по приоритетам доступных ему стратегий и выбор из них наилучшей.
Пусть задача принятия решения задана в виде матрицы 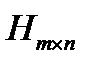 причем игрок выбирает строку в матрице, из которой и определяется его выигрыш. Тогда критерий оптимальности можно понимать как упорядочение " ≥ " на множестве альтернатив, считая, что наилучшей является максимальная по этому упорядочению альтернатива.
причем игрок выбирает строку в матрице, из которой и определяется его выигрыш. Тогда критерий оптимальности можно понимать как упорядочение " ≥ " на множестве альтернатив, считая, что наилучшей является максимальная по этому упорядочению альтернатива.
В теории принятия решений разработан ряд критериев оптимальности, в том числе критерий Вальда, в приложении к играм против природы. [3]. Рассмотрим антагонистическую игру Г=< Х, У, Н>, где X, У -множества стратегий игроков I и II соответственно, а Н - матрица выигрыша игрока I (проигрыша игрока II). В соответствии с принципом максимина игрок I стремится выбрать такую стратегию х°, чтобы при самом неблагоприятном для него выборе игрока II получить наибольший выигрыш, который определяется равенством:
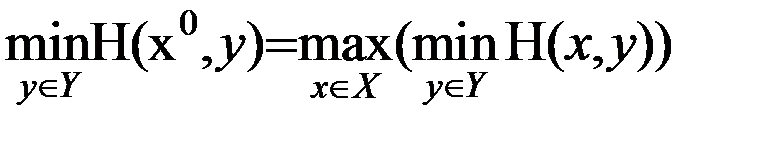 ,
,
где Н(х, у) - элемент матрицы выигрышей Н, соответствующий выбору игроком I стратегии " х", а игроком II - стратегии " у".
Для игрока II, выигрыш равен элементу матрицы Н со знаком минус. При использовании критерия Вальда, он предпочтет стратегию у°, которая обеспечит для него наибольший выигрыш при наименее благоприятном выборе игрока I:
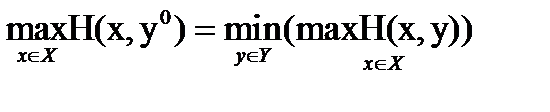
Ситуация (х°, у°) называется ситуацией равновесия в чистых стратегиях если для любых 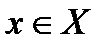 и
и 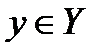 выполнено неравенство седловой точки.
выполнено неравенство седловой точки.
].
Вопросы к зачету
1.Схема обобщенной процедуры системного анализа.
2.Условия принятия решении в исследовании операций.
3.Этапы исследования операций:
4 Простейшие операции в исследовании операци
5. Содержаниие операции на основе принципа гарантированного. результата
6.Статистическая постановка задачи принятия решений
7. Содержательный пример задачи принятия решений в задаче проверки статистических гипотез
8. Однокритериальные.многокритериальные и матричные механизмы выбора.
9 Введение в задачи дифференциальных игр.
10.Динамический аспект дифференциальных игр.
11.Опреление и математическая запись функции выигрыша в дифференциальных играх.
12.Солержательная постановка(концептуалльная структура) задачи на основе принципа гарантированного результата.
13.Разработка математической постановки задачи.принятия решений на основе принципа гарантированного результата
14.Разработка математической постановки задачи.приятия решений на основе принципа гарантированного результата
15. Антагонистическая игра задаваемая тройкой
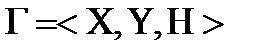 .
.
16.Биматричная антагонистическая игра.
, 18. Выбор оптимальной статегии.