Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическая модель прямой задачи
|
|
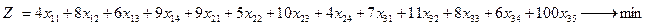при условии что,
| 
|
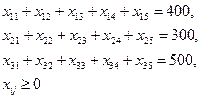
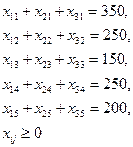
Математическая модель двойственной задачи:
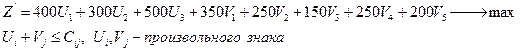
Экономический смысл переменных:
Z – целевая функция прямой задачи (суммарные затраты);
Z ' – целевая функция двойственной задачи (суммарная потенциальная прибыль от перевозки груза);
Сij – стоимость перевозки единицы продукции из i-го пункта в j-ый;
Xij – объем перевозок от i-го поставщика j-му потребителю;
Ui – условная плата перевозчику за вывоз единицы груза из i-го пункта отправления;
Vj – условная плата перевозчику за доставку единицы груза в j-ый пункт назначения.
| Потребители Поставщики | В1 | В2 | В3 | В4 | В5 | Ui | |||
| А1 | 350 4 | 8 | 50 -W | +W | U1 =-2 | ||||
| 6 | 9 | 0 | |||||||
| А2 | 9 | 100 +W | 200 | -W 0 | U2= -6 | ||||
| 5 | 10 | 4 | |||||||
| А3 | 7 | 150 | -W | 100 | +W 8 | 250 6 | 0 | U3 =0 | |
| 11 | |||||||||
| Vj | V1 =6 | V2 =11 | V3 =8 | V4 =6 | V5 = 6 | W=50 |
Проверяем на вырожденность:
R=m+n-1=3+5-1=7
m= 3 – количество поставщиков;
n = 5 – количество потребителей.
Базисных клеток 7, план не вырожден.
Проверяем план на оптимальность, используя метод потенциалов. Для базисных клеток составляем систему уравнений Ui + Vj = Сij находим значение потенциалов так как переменных на 1 больше, чем уравнений,
то переменной U3 присваиваем значение 0 и решаем систему уравнений, получаем
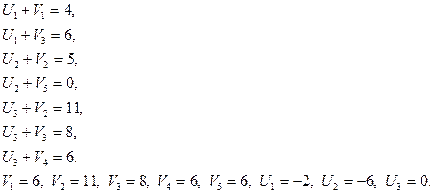
Проверяем выполнение неравенства в свободных: клетках Ui + Vj ≤ Сij
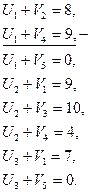
более всего не выполняется условие Ui + Vj ≤ Сij, сюда ставим «+W», строим контур перераспределения W и находим его значение:
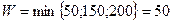Перераспределяем W=50 по контуру.
Составляем следующий план:
| Потребители Поставщики | В1 | В2 | В3 | В4 | В5 | Ui | |||
| А1 | 350 | -W | 50 +W | U1 =-6 | |||||
| 4 | 8 | 6 | 9 | 0 | |||||
| А2 | 9 | 150 +W | 150 | -W 0 | U2= -6 | ||||
| 5 | 10 | 4 | |||||||
| А3 | +W | 100 | -W | 150 8 | 250 6 | 0 | U3 =0 | ||
| 7 | 11 | ||||||||
| Vj | V1 =10 | V2 =11 | V3 =8 | V4 =6 | V5 = 6 | W=100 |
Так как переменных на i больше, чем уравнений, то переменной U3 присваиваем значение 0 и решаем систему уравнений, получаем
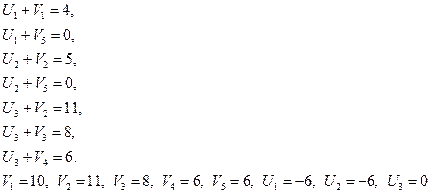
проверяем выполнение неравенства в свободных клетках Ui + Vj ≤ Сij,
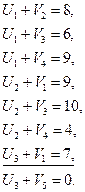
– более всего не выполняется условие Ui + Vj ≤ Сij, сюда ставим «+W», строим контур перераспределения W и находим его значение: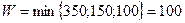 
перераспределяем W=100 по контуру.
Составляем следующий план:
| Потребители Поставщики | В1 | В2 | В3 | В4 | В5 | Ui | |
| А1 | 250 4 | 8 | 6 | 9 | 150 0 | U1 =-3 | |
| А2 | 9 | 250 5 | 10 | 4 | 50 0 | U2= -3 | |
| А3 | 100 7 | 11 | 150 8 | 250 6 | 0 | U3 =0 | |
| Vj | V1 =7 | V2 =8 | V3 =8 | V4 =6 | V5 = 3 |
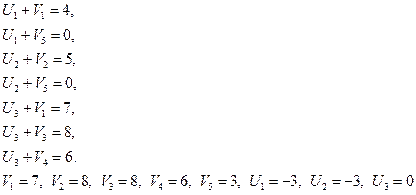
Проверяем выполнение неравенства Ui + Vj ≤ Сij, в свободных клетках:
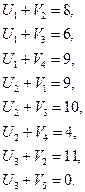
Неравенство Ui + Vj ≤ Сij, в свободных клетках выполняется, построенной план является оптимальным.
Анализ решения.
1. Оптимальный план перевозки продукции:
– от поставщика А1 перевозится 250 ед. продукции потребителю В1; 150 ед. продукции остается у поставщика;
– от поставщика А2 перевозится 250 ед. продукции потребителю В2; 50 ед продукции остается у поставщика;
– от поставщика А3 перевозится 100 ед.продукции потребителю В1, 150 ед, потребителю В3, 250 ед. потребителю В4.
2.Суммарные затраты на изготовление и перевозку продукции:
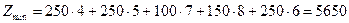ден. ед.
Контрольные вопросы.
1.Как сформулировать постановку транспортной задачи?
2.Какие величины в математической модели транспортной задачи постоянные и какие переменные?
3.Как составить математическую модель прямой и двойственной транспортной задачи?
4.Какая клетка в плане транспортной задачи называется «базисной» и какая «свободной»?
5.Приведите пример сбалансированной и несбалансированной транспортной задачи. Как сбалансировать исходный план транспортной задачи?
6.Поясните понятие «вырожденность» и «невырожденность» плана. Как построить «невырожденный» план?
7.Алгоритм метода наименьшего (наибольшего) элемента.
8.Метод потенциалов и его алгоритм.
9.Какой план транспортной задачи называется опорным?
10.Какой критерий оптимальности плана транспортной задачи?
11.Поясните понятие «коэффициент перераспределения груза – W» и как он определяется?
12.Как построить контур перераспределения W?
13.Анализ решения транспортной задачи.