К выполнению контрольной работы №1

Методические указания к решению задачи №1

Решение этой задачи требует знания закона Ома для всей цепи и ее участков, законов последовательного и параллельного соединения и методики определения эквивалентного сопротивления цепи при смешанном соединении резисторов. Для этого изучите стр.17-21, 53-60 в [1].

Перед решением задачи рассмотрите типовой пример 1.

Пример 1. Цепь постоянного тока содержит резисторы, соединенные смешанно. Схема цепи с указанием резисторов приведена на рис.1а. Всюду индекс тока или напряжения совпадает с индексом резистора, по которому проходит этот ток или на котором действует это напряжение. Например, через резистор R₃ проходит ток I₃ и на нем действует напряжение U₃.

Заданы подведенное напряжение U = 160В, R₁ = 5 Ом, R₂ = 4 Ом, R₃ = 10 Ом, R₄=6 Ом, R₅=3 Ом. Определить токи и напряжения во всех элементах схемы, мощность, потребляемую всей цепью, а также расход электроэнергии за 5 часов работы.

Рис.1а. I₅ R₅

в

I₄ R₄

I₃

R₃

a c

A I₁ R₁ I₂ R₂ B

Дано: R₁ = 5 Ом

R₂ = 4 Ом

R₃ =10 Ом

R₄ = 6 Ом

R₅ = 3 Ом

U_AB = 160 В

t = 5 ч

Определить: I₁, I₂, I₃, I₄, I₅, U_1, U_2, U_3, U_4, U_5, Р, W.

Решение: Обозначим стрелками направление тока в каждом резисторе.

1. Определяем сопротивление параллельно соединенных резисторов R₄ и R₅:

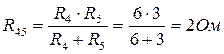
Схема цепи принимает вид, показанный на рис 1б.

Рис.1б.

I₄₅ R₄₅

I₃

R₃

I₁ R₁ a I₂ R₂ c

A B

2. Резисторы R₄₅ и R₃ соединены последовательно, их общее сопротивление:

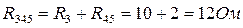
Схема цепи после упрощения приведена на рис.1в.

Рис.1в.

I₃ R₃₄₅

I₁ R₁ a I₂ R₂ c

A B

2. Резисторы R₂ и R₃₄₅ соединены параллельно, их общее сопротивление:

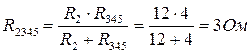
Схема будет иметь вид, показанный на рис.1г.

Рис.1г.

A I₁ R₁ R₂₃₄₅ B

4. Находим эквивалентное (общее) сопротивление всей цепи (см. рис.1д).

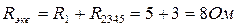
Находим общий ток I₁:

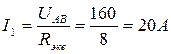
5. Находим напряжение U₁ на R₁:

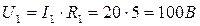
6. Определяем напряжение U_ас на резисторе R₂:

7. Находим ток I₂ в резисторе R₂:

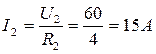
8. Определяем ток I₃ в резисторе R₃:

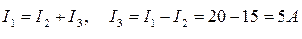
9. Определяем напряжение U₃ на резисторе R₃:

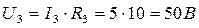
10. Находим напряжение на резисторах R₄ и R₅:

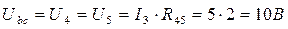
11. Определяем токи в резисторах R₄ и R₅:

12. Рассчитываем мощность, потребляемую всей цепью:

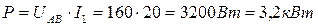
13. Расход энергии за 5 часов работы равен:

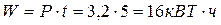
Ответ: I₁=20 А, U₁=100 B Р= 3, 2 кВт.

I₂=15 А, U₂=60 B W=16 кВт·ч.

I₃=5 А, U₃=50 B

I₄=1, 7 А, U₄=10 B

I₅=3, 3 А, U₅=10 B

Методические указания к решению задачи 2

Решение задач этой группы требует знаний учебного материала по методам расчета сложных цепей постоянного тока. Ознакомьтесь с материалом на стр. 74-94 в [1]. Перед решением задачи рассмотрите типовой пример 2.

Пример 2. Для электрической цепи постоянного тока определить токи в ветвях. ЭДС Е₁ = 1, 8 В; Е₂ = 1, 2 В; сопротивления резисторов: R₁ = 0, 2 Ом; R₂ = 0, 3 Ом; R₃ = 0, 8 Ом; R₀₁ = 0, 6 Ом; R₀₂ = 0, 4 Ом.

Дано: Е₁=1, 8 В

Е₂=1, 2 В

R₁=0, 2 Ом

R₂=0, 3 Ом

R₃=0, 8 Ом

R₀₁=0, 6 Ом

R₀₂=0, 4 Ом

Определить: I₁, I₂, I₃

Решение:

Данную схему можно рассчитать несколькими методами.

I. Метод законов Кирхгофа.

Рис.2a.

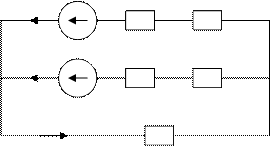a I₁ E₁ R₀₁ R₁ в

f c

I₂ E₂ R₀₂ R₂

e I₃ R₃ d

1. Выберем опорные точки a, b, c, d, e, f и произвольно укажем направление токов I₁, I₂, I₃.

2. Данная цепь имеет 2 узла и 3 ветви. Следовательно, нужно составить 1 уравнение по первому Закону Кирхгофа и 2 по второму.

3. Для узла f: I₁+I₂=I₃ (по первому закону Кирхгофа).

4. Выберем 2 контура: a-b-c-d-e-f-a и f-c-d-e-f.

5. Пусть направление обхода контуров против часовой стрелки, тогда:
Е₁=R₀₁I₁+R₁I₁+R₃I₃= (R₀₁+R₁)I₁+R₃I₃, т.е. 1, 8=(0, 6+0, 2)I₁+0, 8I₃; 1, 8=0, 8I₁+0, 8I₃.

6. Аналогично Е₂=(R₀₂+R₂)I₂+R₃I₃; 1, 2=0, 7I₂+0, 8I₃.

7. В результате совместного решения полученной системы трех уравнений определяем ток I₁ в первой ветви: 1, 8=0, 8I₁+0, 8(I₁+I₂); 1, 8=1, 6I₁+0, 8I₂; 1, 2=0, 7I₂+0, 8(I₁+I₂); 1, 2=1, 5I₂+0, 8I₁ или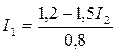

8. Ток второй ветви I₂ находим по значению тока I₁ из уравнений ЭДС Е₁ и Е₂ в соответствии с выражением:

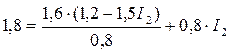; 1, 8=2, 4 – 3I₂+0, 8I₂, откуда

9. Ток в первой ветви I₁ определяют по значению тока I₂ из уравнения для ЭДС Е₁, откуда 1, 8=1, 6I₁+0, 8· 0, 27 или 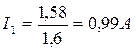, а ток третьей ветви I₃ – из уравнения для токов: I₁+I₂=0, 99+0, 27=I₃, откуда I₃=1, 26 А.

II. Метод двух узлов.

Рис.2б.

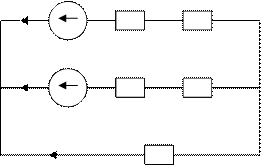I₁ R₀₁ R₁

I₂ R₀₂ R₂

А В

I₃ R₃

1. Примем за положительное направление токов во всех ветвях направление от узла В к узлу А. Определим узловое напряжение:

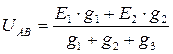, где g₁, g₂, g₃ – проводимости ветвей.

2. Найдем проводимости:

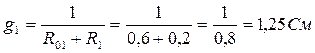
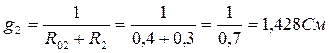
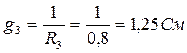
3. Узловое напряжение:

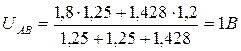
4. Определим токи в ветвях:

I₁ = (E₁ – U_AB)g₁=(1, 8 – 1)·1, 25=1 A,

I₂ = (E₂ – U_AB)g₂=(1, 2 – 1)·1, 428=0, 25 A,

I₃= – U_AB g₃= – 1·1, 25=-1, 25 A.

Проверка: по первому закону Кирхгофа имеем: I₁+I₂+I₃=0

1 + 0, 25 – 1, 25=0.

Примечание. Если какая-либо ЭДС имеет противоположное направление, то в формулы она войдет со знаком “минус”..

III. Метод контурных токов.

Данный метод меньшего числа расчетных уравнений по сравнению с двумя предыдущими.

Рис.2в.

I₁ E₁ R₀₁ R₁

a b

I₂ E₂ R₀₂ R₂

f c

I₃ R₃

e d

1. Разбиваем схему на элементарные контуры: a-b-c-f-a и f-c-d-e-f. Будем считать, что по первому из контуров течет контурный ток I_I, по второму – контурный ток I_II (направление обоих токов против часовой стрелки).

2. Для каждого контура составим уравнение по второму закону Кирхгофа: E_I=I_IR₁₁ – I_IIR₁₂, E_II=I_IIR₂₂ – I_IR₂₁, где E_I, E_II – контурные ЭДС, равные
E_I = E₁ -E₂ = 1, 8 – 1, 2 = 0, 6 В; E_II = E₂=1, 2B

R₁₁, R₂₂ – собственные сопротивления контуров:
R₁₁=R₀₁+R₁+R₀₂+R₂=0, 6+0, 4+0, 2+0, 3= 1, 5 Ом,
R₂₂=R₀₂+R₂+R₃=0, 4+0, 3+0, 8=1, 5 Ом.

R₁₂=R₂₁ – общее сопротивление смежных контуров,

R₁₂ = R₂₁ = R₀₂+R₂=0, 4+0, 3=0, 7 Ом.

3. 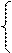Решаем систему:

0, 6=1, 5I_I – 0, 7I_II

1, 2=1, 5I_II – 0, 7I_I

Из первого равенства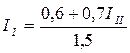

Подставляя во второе: ,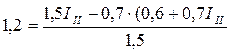

находим I_II=1, 26 А и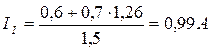

4. Находим токи ветвей через контурные токи:

I₁= I_I=0, 99 A, I₂=I_II - I_I=1, 26 – 0, 99=0, 27 A, I₃=I_II=1, 26 A.

Ответ: I₁=0, 99 A,

I₂=0, 27 A,

I₃=1, 26 A.

Методические указания к решению задачи 3

Решение этой задачи требует знания методики расчета магнитной цепи. Ознакомьтесь с материалом на стр. 202-210. Перед решением задачи рассмотрите типовой пример 3.

Пример 3. Магнитопровод собран из 5 частей электротехнической стали Э42. Длины участков: l₁=l₃=80 мм; l₂=100 мм; l₄=40 мм; l₅=55 мм; S₁=10 см²; S₂=8 см²; S₃=4 см²; S₄= S₅=9 см². Определить ток I в катушке, имеющей w=1000 витков, чтобы поток Ф=7·10^-4 Вб.

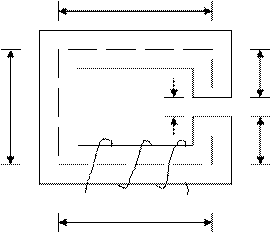l₃

l₄

l₂ l₀

l₅

l₁

Рис.3.

Решение:

1. Определяем магнитную индукцию на каждом участке магнитной цепи:

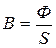
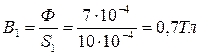
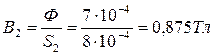
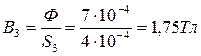
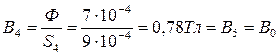
2. Определяем напряженность МП и магнитное напряжение в воздушном зазоре:

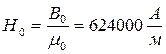
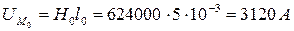
3. По кривым намагничивания находим напряженности МП остальных участков: Н₁=84 А/м, Н₂=130 А/м, Н₃=11900 А/м, Н₄=Н₅=105 А/м.

4. Находим магнитные напряжения участков:
Uм₁= Н₁l₁=84·0, 08=6, 72 A, Uм₂= Н₂l₂=130·0, 1=13 A, Uм₃=Н₃l₃=11900·0, 08=952 A, Uм₄= Н₄l₄=105·0, 04=4, 2 A,
Uм₅= Н₅l₅=105·0, 055=5, 8 A.

5. Определяем общую намагничивающую силу:
F_нс = Uм₁+Uм₂+Uм₃+Uм₄+Uм₅+Uм₀=4101 А.

6. Определяем ток катушки:
F_нс =Iw; I= F_НС/w =4101/1000=4, 1 А.

Примечание. Если воздушного зазора не было, т.е. Н₀=0, то для создания такого же магнитного потока потребовалось бы сила тока: F_нс=4101 – 3120=981 А,
I= F_НС/w = 981/1000 = 0, 981 А.

Методические указания к решению задачи 4

Решение этой задачи требует знания методики расчета разветвленной цепи переменного тока. Ознакомьтесь с материалом на стр. 292-302 в [1]. Перед решением задачи рассмотрите типовой пример 4.

Пример 4. К цепи, показанной на рисунке приложено напряжение U=50 В. Найдите токи во всех ветвях цепи, ток I в неразветвленной части цепи, активную, реактивную и полную мощности цепи, если параметры ее равны X_L1=5 Ом, X_L2=6 Ом, R₂=8 Ом. Постройте векторную диаграмму и определите cosφ всей цепи.

Рис.4.

I

I₁ I₂

X_L2

X_L1

R₂

Дано: U=50 В,

X_L1=5 Ом,

X_L2=6 Ом,

R₂=8 Ом.

Найти: I, I₁, I₂, P, Q, S.

Решение:

1. Полное сопротивление первой ветви Z₁= X_L1 =5 Ом. Полное сопротивление второй ветви .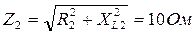

2. Коэффициенты мощности ветвей: ; ; ; .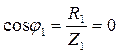

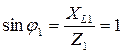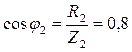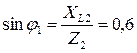3. Найдем токи ветвей: , .

4. Найдем активные и реактивные составляющие тока I₁ и I₂: I_а1= I₁cos φ ₁=0, I_а2= I₂cos φ ₂=5·0, 8=4 А; I_р1= I₁sin φ ₁=10·1= 10 А, I_р2= I₂sin φ ₂=5·0, 6= 3 А.

5. Находим общий ток: .

6. Вычислим активную мощность: Р= I²_а2R₂= 4²·8 = 128 Вт.

7. Находим реактивную и полную мощность:
Q=Q_L1 + Q_L2 = I_р1²X_L1+ I_р2²X_L2 = 10²·5+3²·6=500+54=554 ВАР;

8. Коэффициент мощности цепи: .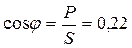

9. Построим векторную диаграмму в масштабе.

Масштаб по напряжению: М_U =10 В/см.

Масштаб по току: М_I =2 А/см.

Длины векторов: , , , , .

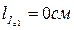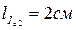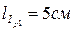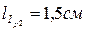U

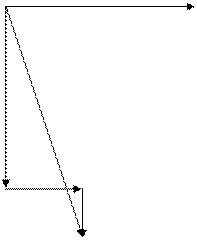
I_p1 = I₁ I

I_a2

I_p2

I₂