
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
К выполнению контрольной работы №2
|
|
Методические указания к решению задачи 1
Решение этой задачи требует знания методики расчета трехфазной цепи с симметричным потребителем, соединенным «звездой» или «треугольником». Ознакомьтесь с материалом на стр. 370-377 в [1]. Перед решением задачи рассмотрите типовой пример 1.
Пример 1. Найти фазные и линейные токи, активную, реактивную, полную мощности фаз и всего приемника, коэффициент мощности. Построить векторную диаграмму, если Rф =3 Ом, Хф =4 Ом, Uл =220 В, потребители соединены в “треугольник”.
Рис.5.
А
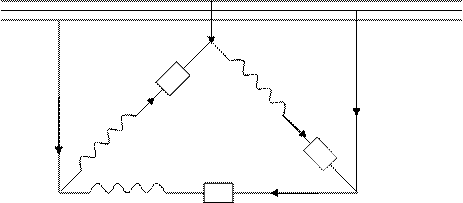 В
В
С
A IA
Rф Xф
ICA IB
Xф IAB
IC Rф
Xф Rф
C B
IBC
Решение:
1. Т.к. соединение D, то 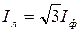 ; Uф = Uл =220 B
; Uф = Uл =220 B
2. Сопротивление каждой фазы 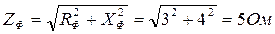 .
.
3. Т.к. нагрузка симметричная, то достаточно произвести расчет только для одной фазы:
Фазный ток:
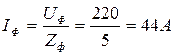 ;
;
Линейный ток:
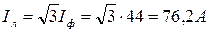 .
.
Коэффициент мощности:
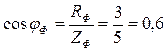 ;
;
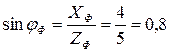 .
.
4. Мощности фаз:
Рф= Iф× Uф× cos jф= 44× 220× 0, 6 = 5808 Вт;
Qф= Iф× Uф× sin jф = 44× 220× 0, 8 =7744 ВАР;
Sф= Iф× Uф = 44× 220 = 9680 ВА.
5. Активная, реактивная, полная мощности всего приемника в 3 раза больше, чем мощность одной фазы:
P=3× Рф = 3× 5808 = 17424 Вт;
Q=3× Qф = 3× 7744 = 23232 ВАР;
S= 3× Sф =3× 9680=29040 ВА.
Векторная диаграмма:
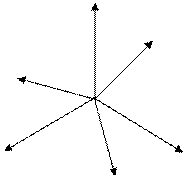 |
UAB
IAB
ICA
UCA IBC UBC
Методические указания к решению задачи 2
Решение этой задачи требует знания методики расчета трехфазной цепи с несимметричным потребителем, соединенным «звездой» или «треугольником». Ознакомьтесь с материалом на стр. 377-386 в [1]. Перед решением задачи рассмотрите типовой пример 2.
Пример 2. К зажимам четырехпроводной сети с линейным напряжением 220 В подключен несимметричный приемник. Сопротивление фаз приемника RА =3 Ом,
XА =4 Ом, RВ = 5 Ом; XС = 10 Ом. Определить фазные токи приемника и ток в нейтральном проводе. Построить векторную диаграмму. Вычислить полную, активную и реактивную мощности каждой фазы и всего приемника, коэффициенты мощности каждой фазы.
Рис.6.
 A
A
B
C
N
RA RB XC
XA
Решение: решим задачу с использованием символического метода.
1. Т.к. соединение «звезда», то 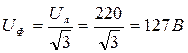 .
.
2. Запишем в комплексном виде фазные напряжения:
UА = 127 В;
UB = 127е-j120°= 127(сos(-120о) +jsin(-120о))=127(сos120о-jsin120о)=127(-0, 5-j0, 87)=
=-63, 5-j110, 5 В;
UC = 127еj120°=127(сos120о + jsin120о) = -63, 5+j110, 5 В.
3. Запишем в комплексном виде сопротивления фаз, а также их модули:
ZA=RА+jXА = 3+j4 =5ej53° Ом; 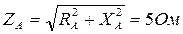 ;
;
ZB = RB = 5 Ом; ZB = 5 Ом; ZС = -jXС = -j10 Ом; ZС = 10 Ом.
4. Вычислим фазные токи:
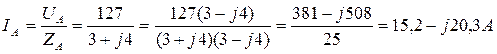
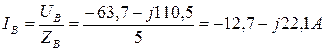
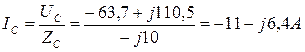 .
.
Ток в нейтральном проводе:
I0 = IA+IB+IC = 15, 2-j20, 3-12, 7-j22, 1-11-j6, 4=-8, 5-j48, 8 A.
5. Коэффициенты мощности фаз:
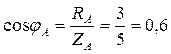 ;
; 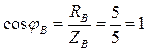 ;
; 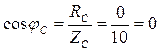 .
.
6. Полная комплексная мощность фаз:
SA = IAUA = 127(15, 2+j20, 3) = 1930, 4+j2578, 1 BA
PA =1930, 4 Вт; QA = 2578, 1 ВАР.
SB = IBUB =(-12, 7+j22, 1)× (-63, 5-j110, 5) = 806, 45+j1403, 35- j1403, 35+2442, 05 =
= 3248, 5 BA.
PB = 3248, 5 Bт; QB = 0 ВАР.
SС = IСUС =(-63, 5+j110, 5)(-11+j6, 4)=698, 5-j406, 4 -j1215, 5-698, 5=-j1621, 9 BA.
PC = 0; QC = -1621, 9 ВАР;
S= SA+ SB+SС =1930, 4+j2578, 1+3248, 5-j1621, 9=5178, 9+j956, 2 BA;
P =5178, 9 Вт; Q = 956, 2 BAР.
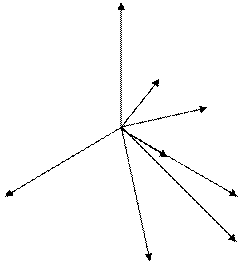 Векторная диаграмма:
Векторная диаграмма:
UA
IA
IAB
IB
UC UB
IC I0
Методические указания к решению задачи 3
Решение этой задачи требует знания методики расчета линейных электрических цепей несинусоидального тока. Ознакомьтесь с материалом на стр. 435-439 в [1]. Перед решением задачи рассмотрите типовой пример 3.
Пример3. Электрическая цепь из последовательно включенных активного сопротивления R= 20 Ом, индуктивности L = 0, 1 Гн и емкости С = 11, 25 мкФ =
= 11, 25× 10-6 Ф питается от источника с напряжением (в вольтах) u = 3 10sin(wt-
-15°) + 77, 5sin3wt + 40sin(5wt +18°45'). Найти мгновенное значение тока в цепи, вычислить действующие значения тока и напряжения, а также активную мощность цепи, если частота первой гармоники f1=50 Гц.
Решение:
1. Применение метода наложения. Заданный источник энергии создает на выводах цепи напряжение, содержащее три синусоидальные составляющие: первую, третью и пятую гармоники. Применяя к заданной линейной цепи метод наложения, можно рассматривать для любого момента времени ток в цепи как результат наложения частичных токов, созданных каждой гармоникой напряжения в отдельности.
Таким образом, в рассматриваемой задаче нужно вычислить полное сопротивление цепи для частот f1, f3 = 3f1 и f5 = 5f1 и найти токи, создаваемые синусоидальными напряжениями (гармониками) этих частот.
2. Вычисление сопротивления цепи.
Индуктивное сопротивление пропорционально частоте, и потому для первой, третьей и пятой гармоник имеем:
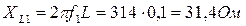 ; XL3 = 3XL1 = 94, 2 Ом; XL5 = 5XL1 =157 Ом.
; XL3 = 3XL1 = 94, 2 Ом; XL5 = 5XL1 =157 Ом.
Емкостные сопротивления для тех же гармоник:
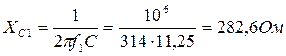
XС3 = XС1/3 = 94, 2 Ом;
XС5 = XС1/5 = 56, 5 Ом.
Полные сопротивления цепи для рассматриваемых гармоник:
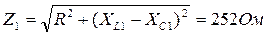 ;
;
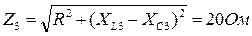 ;
;
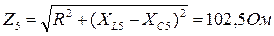 .
.
3. Определение гармоник тока. Для первой гармоники максимальное значение тока:
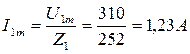
Фазовый сдвиг между напряжением и током первой гармоники определяется по уравнению:
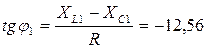 ,
,
откуда:
j1 = - 85o20’.
Поскольку на частоте первой гармоники в цепи преобладает емкостное сопротивление (XC1> XL1), ток опережает напряжение на угол, равный 85o20' и поэтому:
i1=I1msin(w1t - 15o - j1) = 1, 23sin(w1t + 70° 20') А.
Для третьей гармоники максимальное значение тока
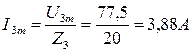 .
.
Сдвиг по фазе между напряжением и током третьей гармоники j3 = 0, так как на этой частоте в цепи устанавливается резонанс напряжений (XL1=XC3). Соответственно:
i3=I3msin3w1t=3, 88sin3w1t A.
Для пятой гармоники имеем:
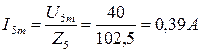 ;
;
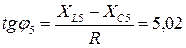 , j5 = 78°45'.
, j5 = 78°45'.
На этот угол (j5) ток пятой гармоники отстает от напряжения, так как в цепи преобладает индуктивное сопротивление (XL5> XC5). Соответственно
i5 = I5msin(5w1t +18o45' - j5)=0, 39sin(5w1t –60о) А.
Мгновенное значение тока найдем наложением гармоник тока в (амперах);
i = i1+i3+i5=1, 23sin(w1t + 70° 20') + 3, 88sin3w1t +0, 39sin(5w1t –60о) А.
4) Вычисление действующих значений тока и напряжения. Действующее значение тока в цепи:
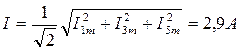 .
.
Действующее значение напряжения источника энергии:
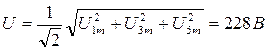 .
.
5. Вычисление активной мощности. Активная мощность цепи складывается из активных мощностей отдельных гармоник, или в нашем случае:
 .
.
Методические указания к решению задачи 4
Решение этой задачи требует знания особенностей протекания переходных процессов в цепях с индуктивностью и емкостью. Ознакомьтесь с материалом на стр. 480-494 в [1]. Перед решением задачи рассмотрите типовые примеры 4, 5.
Пример 4. Катушка индуктивности, соединенная последовательно с сопротивлением R = 30 Ом и включенная в сеть постоянного тока напряжением U = 110 B, мгновенно замыкается накоротко рубильником Р (рис.7). По какому закону будет изменяться ток в катушке после замыкания рубильника, если ее индуктивность L =
= 0, 168 Гн, а сопротивление r =14 Ом?
Решение: До замыкания рубильника ток в катушке не изменялся. Его величина может быть определена по закону Ома: 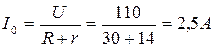
После замыкания рубильника ток в катушке начнет убывать по закону, определяемому уравнением: 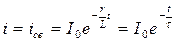
Постоянная времени:
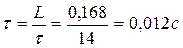
Поэтому: 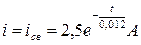 .
.
Пример5. Дана цепь, в которой емкость С = 100 мкФ и сопротивление r =
= 100 Ом соединены последовательно (рис.8). Цепь включается в сеть напряжением U = 220 В. Найти закон изменения тока i и напряжения на конденсаторе uc в зависимости от времени.
Решение: Напряжение и ток конденсатора для любого момента времени будут определяться уравнениями:
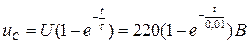 ,
,
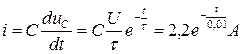 , т.к.
, т.к. 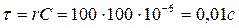 .
.
рис.7. рис.8.















 + +
+ +

 L r r C
L r r C
 U
U

 U
U


 R -
R -

 -
-