Построение доверительных интервалов для среднего.

В MS Excel для вычисления границ доверительного интервала и при числе элементов в выборке п < 30 можно воспользоваться функцией ДОВЕРИТ или процедурой Описательная статистика.

Функция ДОВЕРИТ (альфа; станд_откл; размер) определяет полуширину доверительного интервала и содержит следующие параметры:

- альфа — уровень значимости, используемый для вычисления доверительной вероятности. Доверительная вероятность равняется 100*(1 - альфа)% процентам, или, другими словами, альфа, равное 0, 05, означает 95%-ный уровень доверительной вероятности;

- Станд_откл — стандартное отклонение генеральной совокупности для интервала данных, предполагается известным;

- Размер— это размер выборки.

Пример 2. Найти границы 95%-ного доверительного интервала для среднего значения, если у 25 телефонных аккумуляторов среднее время разряда в режиме ожидания составило 140 часов, а стандартное отклонение — 2, 5 часа.

Решение.

1. Откройте новую рабочую таблицу. Установите табличный курсор в ячейку А1.

2. Для определения границ доверительного интервала необходимо на панели инструментов Стандартная нажать кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ДОВЕРИТ, после чего нажмите кнопку ОК.

3. В рабочие поля появившегося диалогового окна ДОВЕРИТ с клавиатуры введите условия задачи: альфа — 0, 05',

Станд_откл— 2, 5', Размер —25 (рис. 5). Нажмите кнопку ОК.

В ячейке А1 появится полуширина 95%-ного доверительного интервала для среднего значения выборки — 0, 979981. Другими словами, с 95%-ным уровнем надежности можно утверждать, что средняя продолжительность разряда аккумулятора составляет 140 + 0, 979981 часа или от 139, 02 до 140, 98 часа.

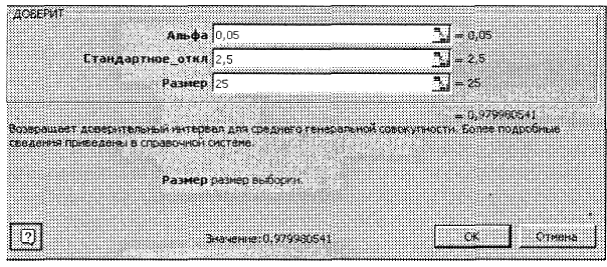
Рис. 5. Пример заполнения диалогового окна ДОВЕРИТ

Пример 3. Пусть имеется выборка, содержащая числовые значения: 13, 15, 17, 19, 22, 25, 19. Необходимо определить границы 95%-ного доверительного интервала для среднего значения и для нахождения «выскакивающей» варианты.

Решение.

1. В диапазон А1: А7 введите исходный ряд чисел.

2. Далее вызовите процедуру Описательная статистика. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика.

3. В появившемся диалоговом окне в рабочем поле Входной и интервал: укажите входной диапазон —А1: А7. Переключателем активизируйте Выходной интервал и укажите выходной диапазон — ячейку В1. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в левое поле Уровень надежности: и в правом поле (%) — 95. Затем нажмите кнопку ОК.

4. В результате анализа в указанном выходном диапазоне для доверительной вероятности 0, 95 получаем значения доверительного интервала (рис. 6).

Рис. 6. Исходная выборка (А1: А7) и результат вычислений (СЗ) из примера

Уровень надежности — это половина доверительного интервала для генерального среднего арифметического. Из полученного результата следует, что с вероятностью 0, 95 среднее арифметического для генеральной совокупности находится в интервале 18, 571 ± 3, 77. Здесь 18, 571— выборочное среднее М для рассматриваемого примера, которое находится обычно процедурой Описательная статистика одновременно с доверительным интервалом.

5. Для нахождения доверительных границ для «выскакивающей» варианты необходимо полученный выше доверительный интервал умножить на n (в примере — 7, то есть 3, 77* 7= 9, 975). В Excel это можно выполнить следующим образом. Табличный курсор установите в свободную ячейку С4; введите с клавиатуры знак =; мышью укажите на ячейку СЗ (в которой находится результат вычислений); введите с клавиатуры знак *; с панели инструментов Стандартная вызовите Мастер функций (кнопка fx); выберите категорию Математические, тип функции Корень; нажмите ОК; введите с клавиатуры число п= 7 и нажмите ОК. В результате получим в ячейке С 4 значение доверительного интервала — 9, 975. Таким образом, варианта, попадающая в интервал 18, 571 ± 9, 975, считается принадлежащей данной совокупности с вероятностью 0, 95. Выходящая за эти границы может быть отброшена с уровнем значимости ά = 0, 05.

УПРАЖНЕНИЯ.

1. По выборке объема п = 9 найдено среднее значение 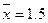. Считая, что генеральная совокупность распределена по нормальному закону с 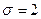, определить интервальную оценку для математического ожидания с надежностью .

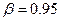Решение. Используя табл. Нормального закона распределения, находим, что

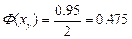
при 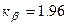. Тогда 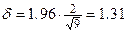и доверительный интервал имеет границы . Таким образом, с вероятностью 0.95 можно быть уверенным в том, что интервал

накроет параметр распределения (математическое ожидание) или, другими словами, с вероятностью 0.95 значение 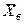дает значение параметра распределения с точностью 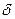= 1.31.

Вычисление величины 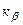, входящей в доверительный интервал:

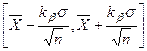
Величина 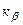вычисляется с помощью функции НОРМСТОБР:

=

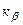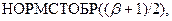
где 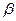– надежность интервальной оценки.

Вычисление величины 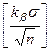осуществляется с помощью функции ДОВЕРИТ:

=

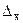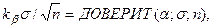
где 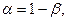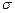– известное среднеквадратичное отклонение, 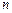– объем выборки. Тогда интервальную оценку можно записать в виде.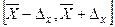

2. По выборке объема п = 9 из нормально распределенной генеральной совокупности найдены значения и 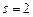. Построить интервальную оценку для математического ожидания с надежностью .

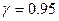Решение. Пользуясь табл. Распределения Стьюдента, находим величину . Тогда точность 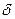определяется соотношением: 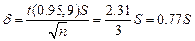, а интервальная оценка имеет границы 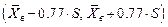, которые зависят от двух случайных величин: 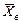и S. Подставляя вместо S ее вычисленное значение s = 2, получаем интервал .

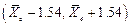Пример 4.

Найти минимальный объем выборки, при котором с доверительной вероятностью 0, 95 ширина доверительного интервала равна 0, 6 при σ _x=1, 2;

Решение:

Ф(t_{0, 4875})=0, 4875; t_{0, 4875}=2, 24 (см. приложение 1);

n=2, 24²·1, 2²/0, 3²=81.

Вывод: минимальный объем равен 81.