
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Магматичні та магматогенно-гідротермальні рудогенеруючі системи, теоретичне та прикладне значення їх геохімічного дослідження.
|
|
Серед ендогенних рудогенерируючих систем найважливіше значення мають магматичні і сполучені з ними магматогенно-гідротермальні. Головні завдання їх геохімічного моделювання можуть бути сформульовані таким чином [15, 20]: 1) визначення провідного механізму формування магматичних серій; 2) встановлення поведінки петрогенних і мікроелементів у процесі магматичної еволюції; 3) оцінка фізико-хімічних, у першу чергу температурних умов функціювання магматичних систем; 4) оцінка їх спроможності до генерації рудоносних флюїдів та формування гідротермально-метасоматичних рудних родовищ; 5) незалежна контрольна перевірка результатів моделювання.
Принципи вирішення завдань 1 і 2 розроблені (Neumann et al., 1954; Рябчиков, 1965, 1975; Gast, 1968; Shaw, 1970; Greenland, 1970; Allegre & Minster, 1978 та ін.) і широко використовуються. Однак вони не забезпечують вирішення завдань 3, 4 і 5. Для їх коректного вирішення автором запропоноване [5, 15, 20, 21, 30, 35 та ін.] комплексне використання розподілу мікроелементів у серіях магматичних порід, експериментальних даних щодо розчинності у силікатних розплавах НАМ [апатиту (Ap), циркону (Zrn) і монациту (Mnz)] та даних про розподіл рідкісних елементів (перед за все Y) в їх асоціаціях.
Принципи і процедура реалізації запропонованого підходу розглянуті на прикладі гранітоїдної серії (рапаківі, граніт-порфіри, жильні граніти) докембрійського (1, 7–1, 8 млрд. років) Коростенського плутону (КП) анортозит-рапаківігранітної формації і рудоносних (Li, Be, Nb, Ta, Zr, W, Sn, Mo, Zn, Pb, Cu, Bi, Cd) метасоматитів Сущано-Пержанської зони (СПЗ), що просторово асоціюють з магматитами КП у межах північно-західної частини УЩ. Побудована геохімічна модель [15, 20, 21, 30 та ін.] ґрунтується на створених аналітичних банках даних “породного” і “мінерального” рівнів і може бути резюмована в такий спосіб:
1. Розподіл мікроелементів у петротипах гранітоїдної серії КП співставлений (рис. 6) з відомими (Neumann et al., 1954; Рябчиков, 1965, 1975; Shaw, 1970; Greenland, 1970; Allegre & Minster, 1978 тощо) моделями їх поведінки у вміщуючих розплав системах — фракційної кристалізації (1), рівноважної кристалізації/плавлення (2), плавлення з безперервним вилученням розплаву та його накопиченням в резервуарі (3), фракційного часткового плавлення (4). При цьому використані відповідні рівняння, спрощені для випадку постійних значень комбінованого коефіцієнта розподілу (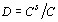 , де
, де 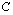 і
і 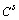 — концентрація елемента в рідкій і твердій фазах системи відповідно). Для застосованих індикаторних елементів (Rb і Sr) з урахуванням емпіричних оцінок (Рябчиков, 1975; Антипин и др., 1984 та ін.) було прийнято:
— концентрація елемента в рідкій і твердій фазах системи відповідно). Для застосованих індикаторних елементів (Rb і Sr) з урахуванням емпіричних оцінок (Рябчиков, 1975; Антипин и др., 1984 та ін.) було прийнято:
D Rb= 0, 5 і D Sr= 2, 0, D Rb= 0, 1 і D Sr= 2, 0, а також D Rb= 0, 1 і D Sr= 0, 1 для умов кристалізації гранітоїдних магм, часткового плавлення на рівні нижньої континентальної кори і верхньої мантії, відповідно. Головним фактором магматичної еволюції був визнаний механізм фракційної кристалізації (1), якому відповідає рівняння Релея (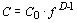 , де
, де 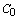 — концентрація елемента у вихідному розплаві,
— концентрація елемента у вихідному розплаві, 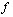 — масова частка рідкої фази в системі). Такий вибір підтверджений і відомим тестом (Рябчиков, 1975) —зворотною лінійною кореляцією ln C Sr (ln C Ba) — ln C Rb , яка випливає з цього рівняння
— масова частка рідкої фази в системі). Такий вибір підтверджений і відомим тестом (Рябчиков, 1975) —зворотною лінійною кореляцією ln C Sr (ln C Ba) — ln C Rb , яка випливає з цього рівняння
Рис. 6. Співставлення даних з геохімії Sr і Rb у гранітоїдах КП, інших комплексів УЩ (Щербаков и др., 1984; Есипчук, 1988) і типових диференційованих комплексів інших регіонів (Богатиков и др., 1987) (сірі кружки і квадрати відповідно) з модельними трендами кристалізації і часткового плавлення. Rbmin , Srmin і Srmax , Rbmax —мінімальні і максимальні концентрації Rb і Sr у ряді породних відмін кожного комплексу. Номери трендів відповідають номерам моделей.
2. Модельні значення 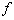 (масова частка залишкового розплаву в глибинній магматичній камері) для кожного різновиду гранітоїдів (його порції) були розраховані як
(масова частка залишкового розплаву в глибинній магматичній камері) для кожного різновиду гранітоїдів (його порції) були розраховані як 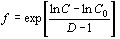 виходячи з концентрацій у петротипах Rb (C Rb) — несумісного елемента з витриманим значенням D Rb = 0, 5 для гранітоїдних систем (Рябчиков, 1975; Антипин и др., 1984 та ін.; наші дані [15]). За концентрацію Rb у вихідному розплаві (
виходячи з концентрацій у петротипах Rb (C Rb) — несумісного елемента з витриманим значенням D Rb = 0, 5 для гранітоїдних систем (Рябчиков, 1975; Антипин и др., 1984 та ін.; наші дані [15]). За концентрацію Rb у вихідному розплаві (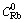 ) прийнята його мінімальна концентрація (169 ppm) у дослідженій серії порід. Зміна концентрацій мікро- і петрогенних (головних) елементів (i) у залишковому розплаві (
) прийнята його мінімальна концентрація (169 ppm) у дослідженій серії порід. Зміна концентрацій мікро- і петрогенних (головних) елементів (i) у залишковому розплаві (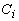 ) у залежності від
) у залежності від 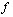 апроксимована, відповідно, рівняннями релеевського (
апроксимована, відповідно, рівняннями релеевського (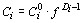 ) (рис. 7 та 9, б) і поліноміального типів, причому з перших випливають оцінки
) (рис. 7 та 9, б) і поліноміального типів, причому з перших випливають оцінки 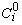 й ефективних значень Di. Ця система рівнянь являє собою ідеалізовану модель поведінки елементів у магматичній еволюції, яка і використовувалася надалі.
й ефективних значень Di. Ця система рівнянь являє собою ідеалізовану модель поведінки елементів у магматичній еволюції, яка і використовувалася надалі.
3. Отримані дані демонструють (рис. 7) зручний для моделювання і досить типовий випадок, коли вихідний розплав був споконвічно насичений щодо головних НАМ — циркону (Zrn) і апатиту (Ap). Насичення щодо монациту (Mnz) і ксенотиму (Xnt) досягалося на наступних етапах його кристалізації, що приводило до послідовної зміни в складі кристалізата ліквідусних парагенезисів Zrn+Ap, Zrn+Mnz, Zrn+Xnt у ході магматичної еволюції. Тому для відповідаючого парагенезису Zrn+Ap діапазону 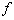 модельна температура (Tmodel) розплаву в момент екстракції його порцій (петротипів) з магматичної камери була розрахована як середнє з оцінок за експериментально отриманими (Watson & Harrison, 1983; Harrison & Watson, 1984) рівняннями розчинності Ap і Zrn:
модельна температура (Tmodel) розплаву в момент екстракції його порцій (петротипів) з магматичної камери була розрахована як середнє з оцінок за експериментально отриманими (Watson & Harrison, 1983; Harrison & Watson, 1984) рівняннями розчинності Ap і Zrn: 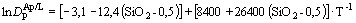 та
та 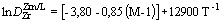 ;
; 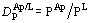 ,
, 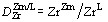 ;
; 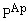 ,
, 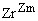 ,
, 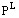 ,
, 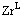 —масові концентрації Zr і P у Zrn, Ap і розплаві відповідно;
—масові концентрації Zr і P у Zrn, Ap і розплаві відповідно; 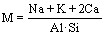 (катіонне відношення в розплаві);
(катіонне відношення в розплаві); 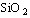 — масова частка
— масова частка 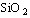 в розплаві;
в розплаві; 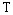 — абсолютна температура (K). У діапазоні парагенезисів Zrn+Mnz і Zrn+Xnt застосовувалося лише друге з них, а оцінки за розчинністю Ap екстраполювалися. В усіх випадках у розрахунках використовувалися модельні параметри складу залишкового розплаву.
— абсолютна температура (K). У діапазоні парагенезисів Zrn+Mnz і Zrn+Xnt застосовувалося лише друге з них, а оцінки за розчинністю Ap екстраполювалися. В усіх випадках у розрахунках використовувалися модельні параметри складу залишкового розплаву.
4. Оцінка вмісту води в залишковому розплаві (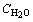 ) для значення f = 0, 185 (заміна Ap на Mnz у парагенезисі з Zrn) отримана підстановкою відповідних модельних оцінок його Tmodel , C LREE і валового складу в рівняння розчинності Mnz (Montel, 1993), яка контролюється не тільки складом та температурою розплаву, але й
) для значення f = 0, 185 (заміна Ap на Mnz у парагенезисі з Zrn) отримана підстановкою відповідних модельних оцінок його Tmodel , C LREE і валового складу в рівняння розчинності Mnz (Montel, 1993), яка контролюється не тільки складом та температурою розплаву, але й 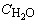 :
: 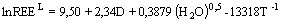 , де
, де 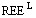 — сума концентрацій у розплаві LREE (La – Gd за винятком Eu), нормованих на їхні атомні маси,
— сума концентрацій у розплаві LREE (La – Gd за винятком Eu), нормованих на їхні атомні маси, 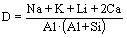 (катіонне відношення в розплаві),
(катіонне відношення в розплаві), 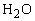 — вміст води (мас. %) у розплаві (
— вміст води (мас. %) у розплаві (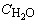 ),
), 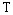 — абсолютна температура (K). Така оцінка, яка в значній мірі базується на Tmodel , дозволяє істотно розвинути модель магматичної системи, у тому числі одержати оцінку
— абсолютна температура (K). Така оцінка, яка в значній мірі базується на Tmodel , дозволяє істотно розвинути модель магматичної системи, у тому числі одержати оцінку 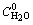 = 2, 36 мас. %, що відповідає (Рябчиков, 1975) виходу первинного розплаву на ліквідус (f = 1) за Tmodel = 900 o і Ptotal ~6, 3 кбар [глибина ~18-20 км, що добре узгоджується з геофізичними даними (Starostenko et al., 2002) щодо залягання покрівлі габроїдного “діапіру” — можливого ініціатора формування первинного розплаву], простежити зростання
= 2, 36 мас. %, що відповідає (Рябчиков, 1975) виходу первинного розплаву на ліквідус (f = 1) за Tmodel = 900 o і Ptotal ~6, 3 кбар [глибина ~18-20 км, що добре узгоджується з геофізичними даними (Starostenko et al., 2002) щодо залягання покрівлі габроїдного “діапіру” — можливого ініціатора формування первинного розплаву], простежити зростання 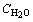 у магматичній еволюції аж до досягнення насичення залишкового розплаву відносно H2O з наступним відокремленням рудоносного водного флюїду (рис. 9), тобто до переходу магматичної системи в магматогенно-гідротермальну стадію розвитку.
у магматичній еволюції аж до досягнення насичення залишкового розплаву відносно H2O з наступним відокремленням рудоносного водного флюїду (рис. 9), тобто до переходу магматичної системи в магматогенно-гідротермальну стадію розвитку.
5. Для оцінки модельних значень коефіцієнта розподілу флюїд/розплав (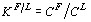 ,
, 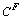 і
і 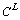 —концентрації елемента у флюїді і розплаві відповідно) тих мікроелементів, інверсії в поведінці яких збігаються з одержаною вище оцінкою (f = 0, 165) досягнення розплавом насичення відносно H2O (рис. 9) та пояснюються їх інтенсивною екстракцією флюїдом, що відокремлювався, використовувався запропонований нами [21] вираз:
—концентрації елемента у флюїді і розплаві відповідно) тих мікроелементів, інверсії в поведінці яких збігаються з одержаною вище оцінкою (f = 0, 165) досягнення розплавом насичення відносно H2O (рис. 9) та пояснюються їх інтенсивною екстракцією флюїдом, що відокремлювався, використовувався запропонований нами [21] вираз:
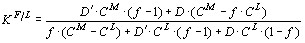 ,
,
де 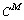 і
і 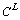 — концентрації елемента в розплаві, розраховані за модельними рівняннями, що описують їх зміну до і після інверсії відповідно, а
— концентрації елемента в розплаві, розраховані за модельними рівняннями, що описують їх зміну до і після інверсії відповідно, а 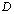 і
і 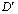 — відповідні їм значення комбінованого коефіцієнта розподілу. Очевидно, що для елементів з монотонною поведінкою (
— відповідні їм значення комбінованого коефіцієнта розподілу. Очевидно, що для елементів з монотонною поведінкою (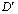 =
= 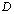 )
) 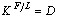 . Повна процедура [21] дозволяє одержати також оцінку масового співвідношення флюїдної і рідкої (розплав) складових системи і масової частки в ній флюїдної фази. Подальші розрахунки [21] дають оцінку складу флюїду (рис. 10, а) у відношенні мікроелементів (
. Повна процедура [21] дозволяє одержати також оцінку масового співвідношення флюїдної і рідкої (розплав) складових системи і масової частки в ній флюїдної фази. Подальші розрахунки [21] дають оцінку складу флюїду (рис. 10, а) у відношенні мікроелементів (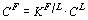 ) [для петрогенних елементів використані експериментально визначені значення
) [для петрогенних елементів використані експериментально визначені значення 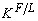 (Чевычелов, Эпельбаум, 1985)], а потім і модельних граничних композицій найбільш високо- і низькотемпературних продуктів його взаємодії з вміщуючими породами:
(Чевычелов, Эпельбаум, 1985)], а потім і модельних граничних композицій найбільш високо- і низькотемпературних продуктів його взаємодії з вміщуючими породами: 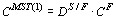 та
та 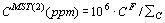 відповідно, де
відповідно, де 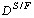 — коефіцієнт розподілу порода/флюїд [прийняті емпіричні оцінки (Антипин и др., 1984)],
— коефіцієнт розподілу порода/флюїд [прийняті емпіричні оцінки (Антипин и др., 1984)], 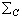 — сума оцінених з моделі масових концентрацій усіх катіонів флюїду. Зіставлення таких модельних оцінок зі складом реальних метасоматитів СПЗ [21] демонструє їх відповідність (рис. 10, б), що підтверджує гіпотезу про генетичний зв'язок цих рудоносних утворень з магматичною системою, що формувала гранітоїдну серію КП.
— сума оцінених з моделі масових концентрацій усіх катіонів флюїду. Зіставлення таких модельних оцінок зі складом реальних метасоматитів СПЗ [21] демонструє їх відповідність (рис. 10, б), що підтверджує гіпотезу про генетичний зв'язок цих рудоносних утворень з магматичною системою, що формувала гранітоїдну серію КП.
Рис. 10. Результати геохімічного моделювання магматогенно-гідротермальної системи гранітоїдів КП: а — зміна модельних концентрацій Zn+Pb+Nb у флюїді (CF ) за період його відокремлення від розплаву; б — модельний склад продуктів функціювання магматогенно-гидротермальної системи (M) і його співставлення зі складом реальних рудоносних метасоматитів СПЗ. L — тренд зміни концентрацій Zn+Pb+Nb у залишковому ро
зплаві; 1 і 2 — графіки зміни значень відповідно 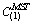 і
і  для Zn+Pb+Nb; стрілка — напрямок зниження температури формування модельних і реальних метасоматитів.
для Zn+Pb+Nb; стрілка — напрямок зниження температури формування модельних і реальних метасоматитів.
6. Серед кількісно оцінених важливих параметрів моделі реальної магматичної і магматогенно-гідротермальної систем КП центральне місце займає Tmodel , коректність оцінки якої визначає надійність усіх наступних модельних побудов. Обов'язковою її умовою є насиченість розплаву відносно Zrn і Ap, що визначає одночасний початок кристалізації і парагенетичні взаємовідносини їх найбільш ранніх мікрокристалів. Це створює умови для реалізації термометрії за такими парагенезисами — важливого незалежного засобу контролю і доповнення Tmodel . Вона заснована на залежності 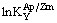 від
від 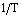 (
(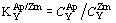 ;
; 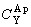 і
і  —масові концентрації Y у Ap і Zrn) [15, 35], для якої встановлений лінійний характер і виконане калібрування на основі геотермометричних оцінок за парагенезисами породоутворюючих мінералів (рис. 11, а), що дозволило запропонувати [20] рівняння для рішення зворотної задачі — оцінки T (
—масові концентрації Y у Ap і Zrn) [15, 35], для якої встановлений лінійний характер і виконане калібрування на основі геотермометричних оцінок за парагенезисами породоутворюючих мінералів (рис. 11, а), що дозволило запропонувати [20] рівняння для рішення зворотної задачі — оцінки T (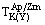 ):
):
(3) 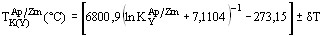 ,
,
де 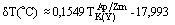 — абсолютна похибка. Для ранніх диференціатів (рис. 8) оцінки
— абсолютна похибка. Для ранніх диференціатів (рис. 8) оцінки 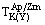 за
за 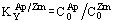 (рис. 11, б) (T початку кристалізації порід) наближаються до оцінок Tmodel (T розплаву в момент його екстракції з магматичної камери) підтверджуючи їх надійність. Для наступних диференціатів закономірно росте значима величина
(рис. 11, б) (T початку кристалізації порід) наближаються до оцінок Tmodel (T розплаву в момент його екстракції з магматичної камери) підтверджуючи їх надійність. Для наступних диференціатів закономірно росте значима величина 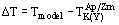 (рис. 8), яка відбиває, можливо, ступінь охолодження при вторгненні цих послідовно зменшувавшихся за обсягом порцій розплаву. Якщо така інтерпретація вірна, то величина
(рис. 8), яка відбиває, можливо, ступінь охолодження при вторгненні цих послідовно зменшувавшихся за обсягом порцій розплаву. Якщо така інтерпретація вірна, то величина 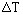 може виявитися інформативною у відношенні рівня глибинності їх кристалізації.
може виявитися інформативною у відношенні рівня глибинності їх кристалізації.
Положення 2. Комплексне використання розподілу елементів-домішок у серіях магматичних гірських порід і в їх циркон-апатитових асоціаціях принципово розширює можливості геохімічного моделювання у відношенні оцінок параметрів і потенційної рудоносності магматичних і сполучених з ними магматогенно-гидротермальних систем (температурний і флюїдний режими, 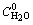 , Ptotal ,
, Ptotal , 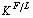 ,
, 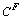 ,
, 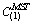 ,
,  тощо), а також значно підвищує надійність усіх модельних оцінок.
тощо), а також значно підвищує надійність усіх модельних оцінок.