
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок выполнения работы. Обработка данных с помощью линейной и сплайновой интерполяции
|
|
Лабораторная работа № 7
Обработка данных с помощью линейной и сплайновой интерполяции
1. Цель: - Изучение способов интерполяции, т.е. перехода от дискретного описания функции к непрерывному, с помощью программ «Mathcad».
Подготовка к работе
Изучить по литературе [1] содержание страниц 397 и по лекции материал по обработке данных.
Литература
[1] - В.И.Каганов. Радиотехника плюс компьютер плюс «Mathcad». М.2001.
Пояснения к работе
При решении многих задач в радиотехнике исходная функция задается в табличной форме или по точкам. Вместе с тем, для дальнейшего анализа, необходимо знать значение функции при любом значении аргумента, а не только при некоторых его дискретных значениях. Данной цели служит процедура аппроксимации. При определении функции между узловыми точками, аппроксимация называется интерполяцией.
«Mathcad» располагает двумя способами такой интерполяции: кусочно-линейной и более точной, называемой сплайновой.
При кусочно-линейной интерполяции вычисление дополнительных точек выполняются по линейной зависимости. Эля этого используется функция «linterp» (VX, VY, x). Для заданных векторов VX и VY узловых точек и заданного аргумента x, функция «linterp» (VX, VY, x) возвращает значение функции при ее линейной аппроксимации. Графически это означает просто соединение узловых точек отрезками прямых.
Сплайн-апроксимация производится отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные. Для осуществления сплайн-апроксимации система «Mathcad» предлагает следующие функции:
- cspline (VX, VY), - возвращает вектор VS вторых производных при приближении в опорных точках отрезками кубических полиномов;
- pspline (VX, VY), - возвращает вектор VS вторых производных при приближении к опорным точкам отрезками парабол;
- lspline (VX, VY), - возвращает вектор VS вторых производных при приближении к опорным точкам отрезками прямой;
- interp (VS, VX, VY, x), - возвращает значение y(x) для заданных векторов VS, VX, VY и значение x.
Сплайн-аппроксимация проводится в два этапа.
Вначале с помощью функций cspline, pspline, или lspline отыскивается вектор вторых производных функции y(x), заданный векторами VX, VY ее абсцисс и ординат. Затем для каждой точки вычисляется y(x) с помощью функции interp.
Порядок выполнения работы
5.1 Произвести кусочно-линейную интерполяцию амплитудной характеристики усилителя, полученной экспериментально в дискретных точках (таблица 1)
Таблица 1
| Uвх(В) | 0, 05 | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 6 | |
| Uвых(В) | 0, 001 | 0, 1 | 0, 2 | 0, 4 | 0, 5 | 0, 55 | 0, 57 | 0, 575 |
В программной среде «Mathcad» исходная функция (Uвых = f (Uвх)) записывается в виде матрицы имеющей 8 строк и 2 столбца
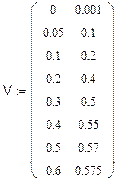
Далее требуется произвести сортировку значений функции по возрастанию значений аргумента (для данного примера, такая сортировка уже выполнена в таблице). Для этого следует обращение к встроенным функциям «f(x)» (например, на стандартной линейке). Сначала записывается
V: =
Затем открывается окно «f(x)», где выбирается категория функции – «сортировка» и имя функции – «сортировка по аргументу» (csort (v, o)).
После щелчка по кнопке «ОК» получена запись
V: = csort (v, o).
Далее следует присвоить значениям аргумента значения 1-го столбца.
X: = V,
а значениям функции значения 2-го столбца.
Y: = V,
Для проведения кусочно-линейной интерполяции следует записать
W(x): =
и открыть окно встроенных функций (f(x)).
В разделе категория функций следует выбрать название «интерполяция», а в разделе «имя функций» - «линейная» («linterp»)
После щелкни по клавише «ОК», появится запись
W: = interp (X, Y, x).
Далее по правилам построения графиков, следует построить график зависимости
W(x) = f(x)
5.2 Выполнить кусочно-линейную интерполяцию вольт-амперной характеристики диода, заданной в дискретных точках (таблица 2).
Таблица 2
| U (В) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| I (mA) | 0.2 | 0.5 |
5.3 Используя сплайн-интерполяции, построить графики зависимостей, приведенных в таблицах 1 и 2. Отличие в записи программы от пункта 5.1 заключается в следующем:
- после записи векторов X: = V и Y: = V
записывается
S: =
и открывается окно встроенной функции (f(x)), в которой в разделе «категория функций» выбирается «интерполяция», а в разделе «имя функции» - «cspline»;
- после щелчка по клавише «ОК» появляется
S: = cspline (▄, ▄)
- вводятся аргумент X и функция Y;
- записывается
W(x): =;
- обращение к f(x) и выбор категории «интерполяция»и имени «interp»;
- щелчок по кнопке «ОК» дает:
W(x): = interp (▄, ▄, ▄, ▄);
- вводятся под знак функции S, X, Y, x.
W(x): = interp (S, X, Y, x)
-строится график функции
W(x) = f(x).
