
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 1. По графику функции путем сдвигов и деформаций построить график функции .
|
|
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
По графику функции 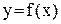 путем сдвигов и деформаций построить график функции
путем сдвигов и деформаций построить график функции 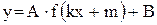 .
.
Построение заданной функции проводится в несколько этапов, которые мы здесь рассмотрим. Функцию 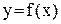 будем называть основной.
будем называть основной.
Построение графика функции 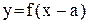 .
.
Предположим, что для некоторых x1 и x2 основная и заданная функции имеют равные ординаты, то есть 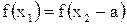 . Но тогда должно быть
. Но тогда должно быть 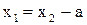 и
и
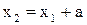 . В зависимости от знака a возможны два случая.
. В зависимости от знака a возможны два случая.
1. Если a > 0, то точка 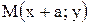 графика функции
графика функции 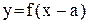 смещена вдоль оси OX на a единиц вправо по сравнению с точкой N(x, y) графика функции f(x) (рис. 3.1).
смещена вдоль оси OX на a единиц вправо по сравнению с точкой N(x, y) графика функции f(x) (рис. 3.1).
2. Если a < 0, то точка 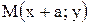 смещена вдоль оси OX на
смещена вдоль оси OX на 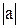 единиц влево по сравнению с точкой N(x, y) графика функции f(x) (рис. 3.2). Таким образом получаем
единиц влево по сравнению с точкой N(x, y) графика функции f(x) (рис. 3.2). Таким образом получаем
 y y
y y
y N(x; y) M(x+a; y) M(x+a; y) y N(x; y)
a 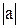
0 x x+a x x+a 0 x x
Рис. 3.1 Рис. 3.2
Правило 1. Если a > 0, то график функции f(x-a) получается из графика основной функции f(x) путем его параллельного переноса вдоль оси OX на “a” единиц вправо.
Если a < 0, то график функции f(x-a) получается из графика основной функции f(x) путем его параллельного переноса вдоль оси OX на 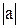 единиц влево.
единиц влево.
Примеры. Построить графики функций: 1) 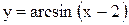 ; 2)
; 2) 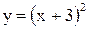 .
.
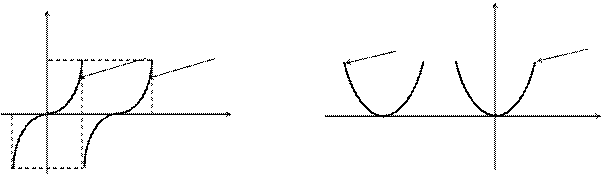
1) Здесь a = 2 > 0. Строим график функции 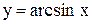 . Сдвинув его на 2 единицы вправо вдоль оси OX, получим график функции
. Сдвинув его на 2 единицы вправо вдоль оси OX, получим график функции 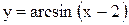
(рис. 3.3).
2) Здесь a = -3 < 0. Строим график функции 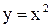 . Сдвинув его на 3 единицы влево, получим график функции
. Сдвинув его на 3 единицы влево, получим график функции 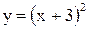 (рис. 3.4).
(рис. 3.4).
 |
Y Y
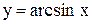
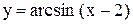 y=(x+3)2 y=x2
y=(x+3)2 y=x2
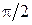
-1 0 1 2 3 x -3 -2 -1 0 1 2 x
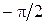
Рис. 3.3 Рис. 3.4
Замечание. Построение графика функции 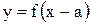 можно выполнить иначе: построив график основной функции
можно выполнить иначе: построив график основной функции 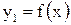 в системе
в системе 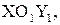 надо перенести ось
надо перенести ось 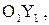 на а единиц влево, если
на а единиц влево, если 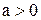 , и на
, и на 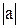 единиц вправо, если
единиц вправо, если 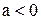 . Тогда в системе
. Тогда в системе 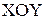 получим график функции
получим график функции 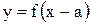 . Система
. Система 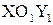 имеет вспомогательное значение, поэтому ось
имеет вспомогательное значение, поэтому ось 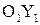 изображается пунктирно или карандашом.
изображается пунктирно или карандашом.
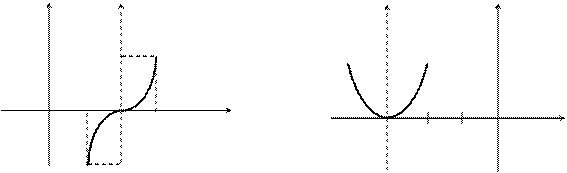
В качестве примера построим еще раз графики функций 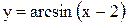 и
и 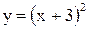 (рис. 3.5) и (рис. 3.6)
(рис. 3.5) и (рис. 3.6)
 Y Y1 Y1 Y
Y Y1 Y1 Y
О1 О
0 1 2 x -3 -2 -1 0 x
Рис. 3.5 Рис. 3.6
Построение графика функции 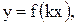 где
где 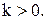
Пусть для некоторых значений 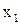 и
и 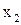 ординаты функций
ординаты функций 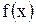 и
и 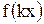 равны, то есть
равны, то есть 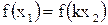 . Тогда
. Тогда 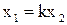 и
и 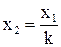 . Таким образом, каждой точке
. Таким образом, каждой точке 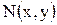 графика основной функции
графика основной функции 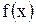 соответствует точка
соответствует точка 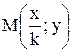 графика функции
графика функции 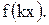 Возможны два случая.
Возможны два случая.
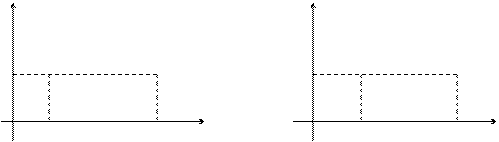
1. Если 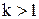 , то точка
, то точка 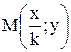 лежит в k раз ближе к оси OY, чем точка
лежит в k раз ближе к оси OY, чем точка 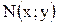
 (рис. 3.7).
(рис. 3.7).
2. Если же 0 < k < 1, то точка 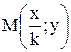 лежит в
лежит в 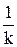 раз дальше от оси OY по сравнению с точкой
раз дальше от оси OY по сравнению с точкой 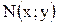 (рис. 3.8). Таким образом, происходит сжатие или растяжение графика функции.
(рис. 3.8). Таким образом, происходит сжатие или растяжение графика функции.
 Y Y
Y Y
y 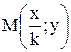
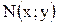 y
y 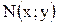
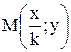
0 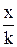 x X 0 x
x X 0 x 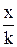 X
X
Рис. 3.7 Рис. 3.8
Правило 2. Пусть k > 1. Тогда график функции f(kx) получается из графика функции f(x) путем его сжатия вдоль оси OX в k раз (иначе: его сжатием к оси OY в k раз).
Пусть 0 < k < 1. Тогда график f(kx) получается из графика f(x) путем его растяжения вдоль оси OX в 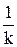 раз.
раз.
Примеры. Построить графики функций: 1) 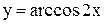 и
и 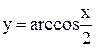 ;
;
2) 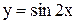 и
и  .
.
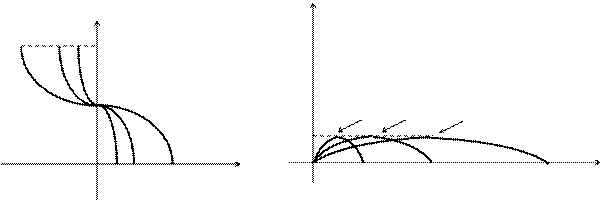 Y Y
Y Y
(3) (1) (2) p
p/2 (2) (1) (3)
1
-2 -1 0 ½ 1 2 x 0 p/2 p 2p x
Рис. 3.9 Рис. 3.10
1. Строим график функции 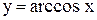 - кривая (1) на рис. 3.9. Сжав его в два раза к оси OY, получим график функции
- кривая (1) на рис. 3.9. Сжав его в два раза к оси OY, получим график функции 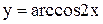 - кривая (2) на рис. 3.9. При этом, например, точка (1; 0) переходит в точку
- кривая (2) на рис. 3.9. При этом, например, точка (1; 0) переходит в точку 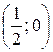 , точка
, точка 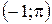 переходит в точку
переходит в точку 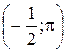 .
.
Замечание. Обратите внимание: точка 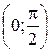 , лежащая на оси OY, остается на месте. Действительно, всякой точке N(0, y) графика f(x) соответствует точка
, лежащая на оси OY, остается на месте. Действительно, всякой точке N(0, y) графика f(x) соответствует точка 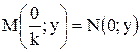 графика f(kx).
графика f(kx).
График функции 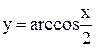 получается растяжением графика функции
получается растяжением графика функции 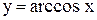 от оси OY в 2 раза. При этом снова точка
от оси OY в 2 раза. При этом снова точка 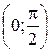 остается без изменения (кривая (3) на рис. 3.9).
остается без изменения (кривая (3) на рис. 3.9).
2. По графику функции 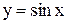 , построенному в промежутке
, построенному в промежутке 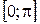 , строим графики функций
, строим графики функций 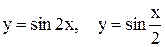 - кривые (1), (2), (3) на рис. 3.10. Обратите внимание, что точка (0; 0) остается неподвижной.
- кривые (1), (2), (3) на рис. 3.10. Обратите внимание, что точка (0; 0) остается неподвижной.
Построение графика функции y=f(-x).
Функции f(x) и f(-x) принимают равные значения для противоположных значений аргумента x. Следовательно, точки N(x; y) и M(-x; y) их графиков будут симметричны относительно оси OY.
Правило 3. Чтобы построить график f(-x), надо график функции f(x) зеркально отразить относительно оси OY.
Примеры. Построить графики функций 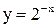 и
и 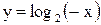 .
.
Решения показаны на рис. 3.11 и 3.12.

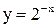 Y
Y  Y
Y
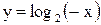
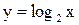
1 -1 1 х
0 x
Рис. 3.11 Рис. 3.12
Построение графика функции y=f(-kx), где k > 0.
Правило 4. Строим график функции y=f(kx) в соответствии с правилом 2. График функции f(kx) зеркально отражаем от оси OY в соответствии с прави-
лом 3. В результате получим график функции f(-kx).
Примеры. Построить графики функций 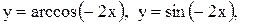
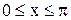 .
.
Решения показаны на рис. 3.13 и 3.14.

 Y Y
Y Y

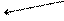

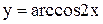 p
p 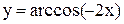

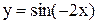
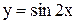
 p/2
p/2


 1
1

 -1/2 0 1/2 x -p/2 0 p/2 x
-1/2 0 1/2 x -p/2 0 p/2 x
Рис. 3.13 Рис. 3.14
Построение графика функции 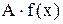 , где A > 0. Если A > 1, то для каждого значения
, где A > 0. Если A > 1, то для каждого значения 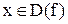 ордината заданной функции в А раз больше, чем ордината основной функции f(x). В этом случае происходит растяжение графика f(x) в А раз вдоль оси OY (иначе: от оси OX).
ордината заданной функции в А раз больше, чем ордината основной функции f(x). В этом случае происходит растяжение графика f(x) в А раз вдоль оси OY (иначе: от оси OX).
Если же 0 < A < 1, то происходит сжатие графика f(x) в 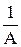 раз вдоль оси OY (или от оси OX).
раз вдоль оси OY (или от оси OX).
Правило 5. Пусть A > 1. Тогда график функции 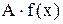 получается из графика f(x) путем его растяжения в А раз вдоль оси OY (или от оси OX).
получается из графика f(x) путем его растяжения в А раз вдоль оси OY (или от оси OX).
Пусть 0 < A < 1. Тогда график функции 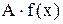 получается из графика f(x) путем его сжатия в
получается из графика f(x) путем его сжатия в 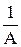 раз вдоль оси OY (или к оси OX).
раз вдоль оси OY (или к оси OX).
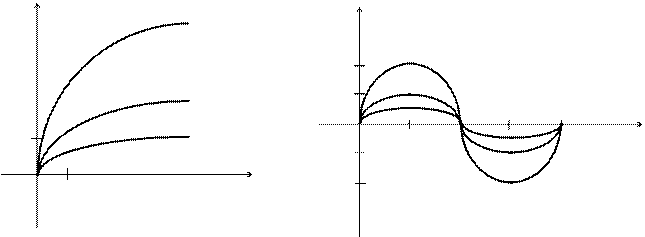
Примеры. Построить графики функций 1) 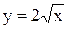 ,
, 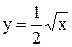 и 2)
и 2) 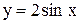 ,
,
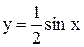 .
.

 Y
Y 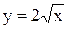 Y
Y 
 2
2 

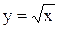 1
1 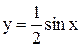
1 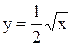 0 p/2 p p/3 p x
0 p/2 p p/3 p x
-1
1 х -2
Рис. 3.15 Рис. 3.16
Построение графика функции 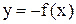 .
.
Для каждого 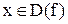 точки N(x, y) функции f(x) и M(x, -y) функции -f(x) симметричны относительно оси OX, поэтому получаем правило.
точки N(x, y) функции f(x) и M(x, -y) функции -f(x) симметричны относительно оси OX, поэтому получаем правило.
Правило 6. Для построения графика функции 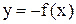 надо график
надо график 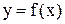 зеркально отразить относительно оси OX.
зеркально отразить относительно оси OX.
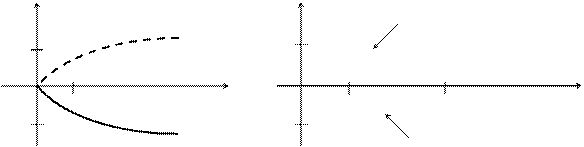
Примеры. Построить графики функций 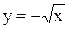 и
и 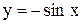 (рис. 3.17 и 3.18).
(рис. 3.17 и 3.18).


 Y Y
Y Y
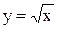 1
1 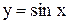
0 1 x 0 π /2 π 3π /2 2π x
-1 -1
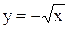
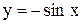
Рис. 3.17 Рис. 3.18
Построение графика функции 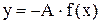 , где A> 0.
, где A> 0.
Правило 7. Строим график функции 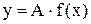 , где A> 0, в соответствии с правилом 5. Полученный график отражаем зеркально от оси OX в соответствии с правилом 6.
, где A> 0, в соответствии с правилом 5. Полученный график отражаем зеркально от оси OX в соответствии с правилом 6.
Построение графика функции 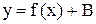 .
.
Если B> 0, то для каждого 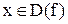 ордината заданной функции на B единиц больше, чем ордината f(x). Если же B< 0, то для каждого
ордината заданной функции на B единиц больше, чем ордината f(x). Если же B< 0, то для каждого 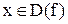 ордината первой функции уменьшается на
ордината первой функции уменьшается на 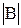 единиц по сравнению с ординатой f(x). Таким образом, получаем правило.
единиц по сравнению с ординатой f(x). Таким образом, получаем правило.
Правило 8. Чтобы построить график функции 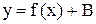 по графику y=f(x), надо этот график перенести вдоль оси OY на В единиц вверх, если B> 0, или на
по графику y=f(x), надо этот график перенести вдоль оси OY на В единиц вверх, если B> 0, или на 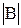 единиц вниз, если B< 0.
единиц вниз, если B< 0.
Примеры. Построить графики функций: 1) 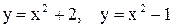 и
и
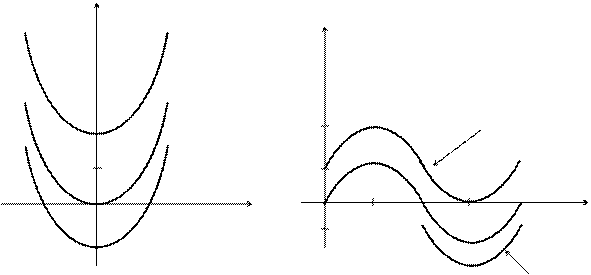 2)
2) 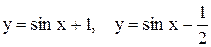 (рис. 3.19 и 3.20).
(рис. 3.19 и 3.20).
Y
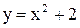 Y
Y
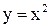
2 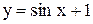
2 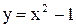
1 1
 |
0 x 0 π /2 π 3π /2 2π x
1/2
-1
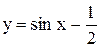
Рис. 3.19 Рис. 3.20
Схема построения графика функции 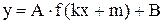 .
.
Прежде всего запишем уравнение функции в виде 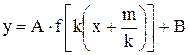 и обозначим
и обозначим 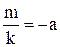 . Тогда график функции
. Тогда график функции 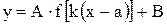 строим по следующей схеме.
строим по следующей схеме.
1. Строим график основной функции f(x).
2. В соответствии с правилом 1 строим график f(x-a).
3. Путем сжатия или растяжения графика f(x-a) с учетом знака k по правилам 2-4 строим график функции f [k(x-a)].
Обратите внимание: сжатие или растяжение графика f(x-a) происходит относительно прямой x=a (почему?)
4. По графику 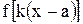 в соответствии с правилами 5-7 строим график функции
в соответствии с правилами 5-7 строим график функции 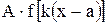 .
.
5. Полученный график сдвигаем вдоль оси OY в соответствии с правилом 8.
Обратите внимание: на каждом шаге построения в качестве графика основной функции выступает предыдущий график.
Пример. Построить график функции 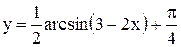 . Здесь k=-2, поэтому
. Здесь k=-2, поэтому 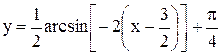 . Учитывая нечетность
. Учитывая нечетность 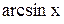 , имеем
, имеем  .
.
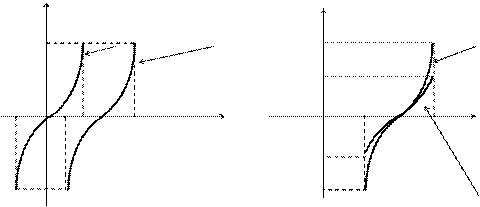
1. Строим график основной функции 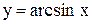 .
.
2. Сместив его вдоль оси OX на  единицы вправо, получим график функции
единицы вправо, получим график функции
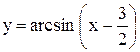 (рис. 3.21).
(рис. 3.21).
3. Полученный график сжимаем в 2 раза к прямой 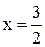 и таким образом получаем график функции
и таким образом получаем график функции 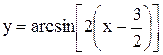 (рис. 3.22).
(рис. 3.22).
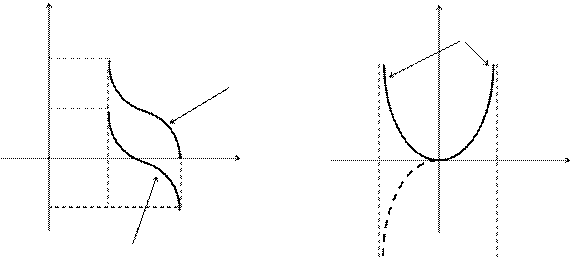
4. Сжав к оси OX последний график в 2 раза и зеркально отразив его от оси OX, получим график функции 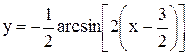 (рис. 3.22 и 3.23).
(рис. 3.22 и 3.23).
5.  Наконец, смещением на
Наконец, смещением на 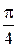 вверх по оси OY получаем график искомой функции (рис. 3.23).
вверх по оси OY получаем график искомой функции (рис. 3.23).
Y Y
π /2 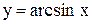
 π /2
π /2 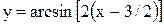
π /4
-1 0 1/2 3/2 x 0 1 3/2 2 x
-π /4
-π /2 -π /2 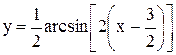
Рис. 3.21 Рис. 3.22
 Y Y
Y Y
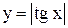
π /2 
π /4
0 1 3/2 2 x -π /2 0 π /2 x
-π /4
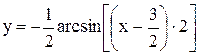
Рис. 3.23 Рис. 3.24