
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 2. Построение графиков функций, содержащих знак модуля.
|
|
Построение графиков функций, содержащих знак модуля.
Решение этой задачи также состоит из нескольких этапов. При этом необходимо помнить определение модуля: 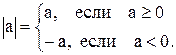
Построение графика функции 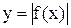 .
.
Для тех значений 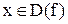 , для которых
, для которых 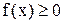 , будет
, будет 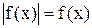 . Поэтому здесь графики функций
. Поэтому здесь графики функций 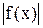 и f(x) совпадают. Для тех же
и f(x) совпадают. Для тех же 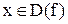 , для которых f(x)< 0, будет
, для которых f(x)< 0, будет 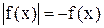 . Но график -f(x) получается из графика f(x) зеркальным отражением от оси OX. Получаем правило построения графика функции
. Но график -f(x) получается из графика f(x) зеркальным отражением от оси OX. Получаем правило построения графика функции 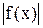 .
.
Правило 9. Строим график функции y=f(x). После этого ту часть графика f(x), где 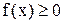 , оставляем без изменения, а ту его часть, где f(x)< 0, зеркально отражаем от оси OX.
, оставляем без изменения, а ту его часть, где f(x)< 0, зеркально отражаем от оси OX.
Замечание. Обратите внимание, что график 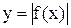 всегда лежит выше оси OX или касается ее.
всегда лежит выше оси OX или касается ее.
Примеры. Построить графики функций 
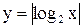 (рис. 3.24, 3.25, 3.26).
(рис. 3.24, 3.25, 3.26).
Y Y 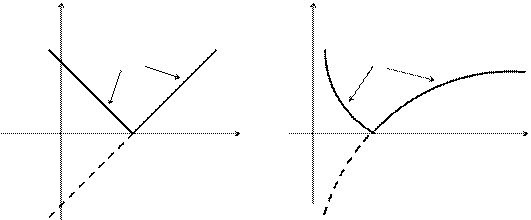
2 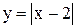
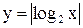
0 2 x 0 x
-2
Рис. 3.25 Рис. 3.26
Построение графика функции 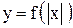 .
.
Так как 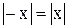 , то
, то 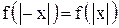 , то есть задана четная функция, график которой симметричен относительно оси OY.
, то есть задана четная функция, график которой симметричен относительно оси OY.
Правило 10. Строим график функции y=f(x) при 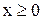 . Отражаем построенный график от оси OY. Тогда совокупность двух полученных кривых даст график функции
. Отражаем построенный график от оси OY. Тогда совокупность двух полученных кривых даст график функции 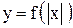 .
.
Примеры. Построить графики функций 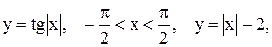
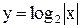 (рис.3.27, 3.28, 3.29)
(рис.3.27, 3.28, 3.29)
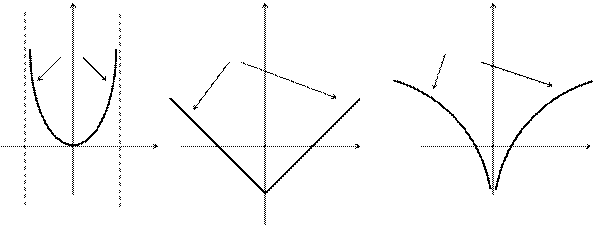 Y Y Y
Y Y Y
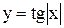
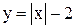
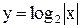
-π /2 0 π /2 x -2 0 2 x -1 1 x
Рис. 3.27 Рис. 3.28 Рис. 3.29
Построение графика функции 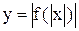 .
.
Строим график функции 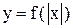 по правилу 10.
по правилу 10.
Строим график функции 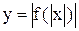 по правилу 9.
по правилу 9.
Примеры. Построить графики функций 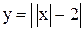 и
и 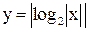 .
.
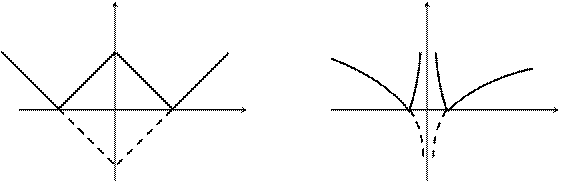
1. Строим график функции 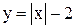 (рис. 3.28)
(рис. 3.28)
Отрицательную часть графика отражаем от оси OX. График 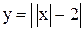 изображен на рис. 3.30.
изображен на рис. 3.30.
 Y Y
Y Y
-2 0 2 x -1 0 1 x
-2
Рис. 3.30 Рис. 3.31
2. Строим график функции 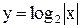 (рис. 3.29).
(рис. 3.29).
Отражаем отрицательную часть графика от оси OX. График 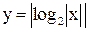 изображен на рис. 3.31.
изображен на рис. 3.31.
При построении графика функции, содержащей знаки модуля, весьма существенно знать промежутки знакопостоянства функции. Поэтому решение каждой задачи необходимо начинать с определения этих промежутков.
Пример. Построить график функции 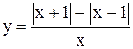 .
.
Область определения 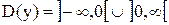 . Выражения x+1 и x-1 изменяют свои знаки в точках x=-1 и x=1. Поэтому область определения разобьем на четыре промежутка:
. Выражения x+1 и x-1 изменяют свои знаки в точках x=-1 и x=1. Поэтому область определения разобьем на четыре промежутка:
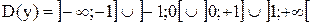 .
.
 |
-1 0 1 x
Учитывая знаки x+1 и x-1, имеем
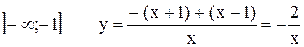 ;
;
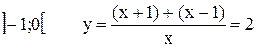 ;
;
 ;
;
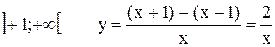 .
.
Таким образом, функцию можно записать без знаков модуля следующим образом:
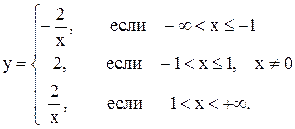
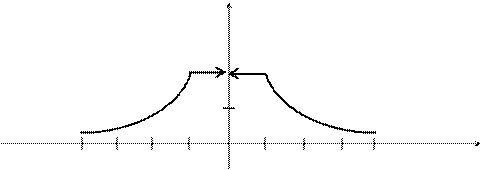
Функциям 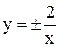 соответствуют гиперболы, а функции y=2 – прямая линия. Дальнейшее построение можно провести по точкам (рис. 3.32).
соответствуют гиперболы, а функции y=2 – прямая линия. Дальнейшее построение можно провести по точкам (рис. 3.32).
| x | -4 | -2 | -1 | - 
| 
| |||
| y | 
| 
|
 Y
Y
-4 -3 -2 -1 0 1 2 3 4 x
Рис. 3.32
Замечание. Обратите внимание, что при x=0 функция не определена. Говорят, что функция в этой точке терпит разрыв. На рис. 3.32 это отмечено стрелками.
Задача 3. Построение графика функции, заданной несколькими аналитическими выражениями.
В предыдущем примере функцию 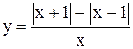 мы представили несколькими аналитическими выражениями. Так, в промежутке
мы представили несколькими аналитическими выражениями. Так, в промежутке 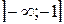
 она изменяется по закону гиперболы
она изменяется по закону гиперболы 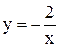 ; в промежутке
; в промежутке 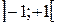 , кроме x=0, это линейная функция; в промежутке
, кроме x=0, это линейная функция; в промежутке 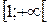 снова имеем гиперболу
снова имеем гиперболу 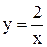 . Подобные функции часто будут встречаться в последующем. Рассмотрим простой пример.
. Подобные функции часто будут встречаться в последующем. Рассмотрим простой пример.
Путь поезда от станции А до станции B состоит из трех участков. На первом участке он набирает скорость, то есть в промежутке 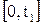 его скорость
его скорость  , где
, где 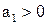 . На втором участке он движется с постоянной скоростью, то есть v=c, если
. На втором участке он движется с постоянной скоростью, то есть v=c, если 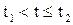 . Наконец, при торможении его скорость будет
. Наконец, при торможении его скорость будет 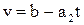 . Таким образом, в промежутке
. Таким образом, в промежутке 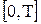 скорость движения изменяется по закону
скорость движения изменяется по закону
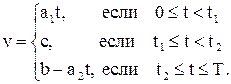
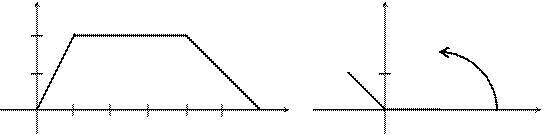
Построим график этой функции, полагая a1=2, c=2, b=6, a2=1 (рис. 3.33).
 V2 Y
V2 Y
1 1
0 1 2 3 4 5 6 x 0 π /2 π x
Рис. 3.33 Рис. 3.34
В этом примере скорость v изменяется непрерывно. Однако в общем случае процесс может протекать более сложно. Так, функция
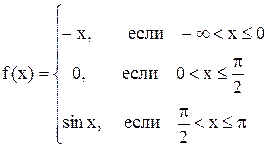
имеет более сложный график (рис. 3.34), который в точке 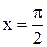 терпит разрыв.
терпит разрыв.
Таким образом, если задана функция
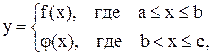
то надо построить график функции y=f(x) в промежутке 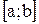 и график функции
и график функции 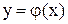 в промежутке
в промежутке 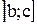 . Совокупность двух таких линий даст график заданной функции.
. Совокупность двух таких линий даст график заданной функции.
Задача 4. Построение кривых, заданных параметрически.
Задание кривой L параметрически характеризуется тем, что координаты x, y каждой точки 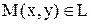 задаются как функции некоторого параметра t:
задаются как функции некоторого параметра t:
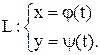 (1)
(1)
При этом в качестве параметра t может выступать время, угол поворота и т.д.
К параметрическому заданию кривой L прибегают в тех случаях, когда трудно или вообще невозможно выразить явным образом y как функцию аргумента x, то есть y=f(x). Приведем некоторые примеры.
Пример 1. Декартовым листом называется кривая L, уравнение которой имеет вид 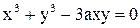 .
.
Положим здесь 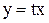 , тогда
, тогда 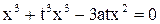 или
или 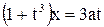 , то есть
, то есть 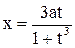 ,
, 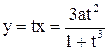 . Итак, параметрические уравнения декартова листа имеют вид:
. Итак, параметрические уравнения декартова листа имеют вид: 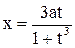 ,
, 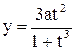 , где
, где 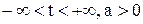 .
.
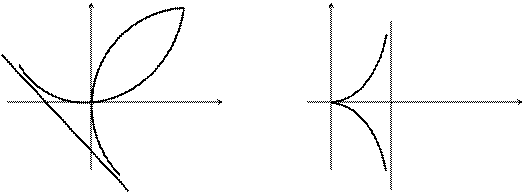
Кривая изображена на рис. 3.35. Она имеет асимптоту y=-a-x.
 Y
Y  Y
Y
-a 0 x 0  2a x
2a x
-a
Рис. 3.35 Рис. 3.36
Пример 2. Циссоидой называется кривая L, заданная уравнением 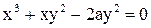 . Полагая здесь x=ty, получим ее параметрические уравнения:
. Полагая здесь x=ty, получим ее параметрические уравнения:
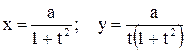 .
.
Циссоида изображена на рис. 3.36. Она имеет асимптоту x=2a.
Построение кривой L, заданной параметрически, выполняется по точкам. При этом рекомендуется следующий план действий.
1. Из уравнений (1) определить промежуток изменения параметра t, а также переменных x и y.
2. Учесть особенности уравнений (1). В частности, если
а) функция 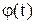 нечетная, а
нечетная, а 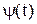 - четная, то есть, если
- четная, то есть, если 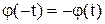 и
и 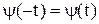 , то график функции (1) симметричен относительно оси OY.
, то график функции (1) симметричен относительно оси OY.
б) функция 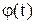 - четная,
- четная, 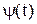 - нечетная, то есть, если
- нечетная, то есть, если 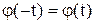 и
и 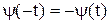 , то график функции (1) симметричен относительно оси OX.
, то график функции (1) симметричен относительно оси OX.
3. Найти точки пересечения кривой с осями координат.
4. Исследовать поведение x и y при 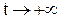 , а также при
, а также при 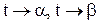 , если
, если  .
.
5. Составить таблицу значений для параметра t, переменных x и y.
6. По координатам (x, y) полученных точек построить кривую.
7.
Пример 3. Построить кривую, заданную уравнениями:
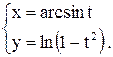
1. Так как 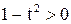 , то
, то 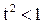 и
и 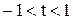 . Тогда из первого уравнения следует, что
. Тогда из первого уравнения следует, что 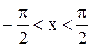 ; а из второго
; а из второго 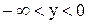 . Итак,
. Итак, 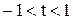 ,
, 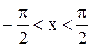 ,
, 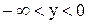 .
.
2. Так как 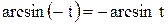 и
и 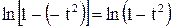 , то кривая симметрична относительно оси OY. Следовательно, достаточно построить кривую при
, то кривая симметрична относительно оси OY. Следовательно, достаточно построить кривую при 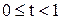 .
.
3. Если x=0, то 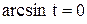 , то есть t=0. Тогда y=0. Таким образом, кривая проходит через начало координат.
, то есть t=0. Тогда y=0. Таким образом, кривая проходит через начало координат.
4. Если 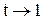 , то
, то 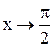 и
и  . Следовательно, прямая
. Следовательно, прямая 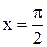 есть асимптота кривой.
есть асимптота кривой.
5. Составляем таблицу значений
6.
| t | 
| 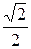
| 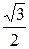
| 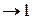
| |
| x | 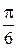
| 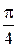
| 
| 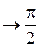
| |
| y | 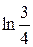
| 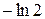
| 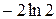
| 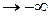
|
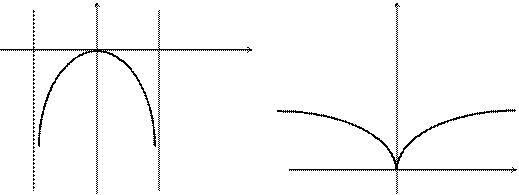
Кривая изображена на рис. 3.37.
 Y Y
Y Y
-π /2 0 π /2 x
0 x
Рис. 3.37 Рис. 3.38
Замечание. Уравнение кривой можно записать в явном виде, если исключить параметр t из обоих уравнений. Так как 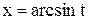 , то
, то 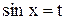 . Подставив это значение t во второе уравнение, получим
. Подставив это значение t во второе уравнение, получим 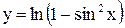 . Таким образом,
. Таким образом, 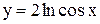 .
.
Пример 4. Построить кривую, заданную уравнениями 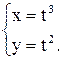
1. Здесь 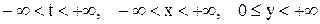 .
.
2. Так как 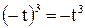 и
и 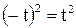 , то кривая симметрична относительно оси OY. Следовательно, график ее строим для
, то кривая симметрична относительно оси OY. Следовательно, график ее строим для 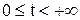 .
.
3. Если x=0, то t=0 и y=0. Кривая проходит через точку O(0; 0).
4. Если 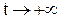 , то
, то 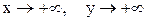 .
.
5. Составляем таблицу значений
| t | 
| 
| |||
| x | 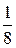
| 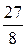
| |||
| y | 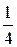
| 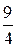
|
Кривая изображена на рис. 3.38. Она называется полукубической параболой. Запишем уравнение этой параболы в явном виде. Так как 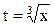 , то
, то 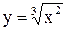 .
.
Задача 5. Построение кривых в полярной системе координат.
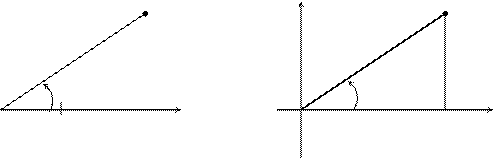
Помимо декартовой прямоугольной системы XOY на плоскости можно определить так называемую полярную систему координат. Ее образует луч 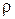 , на котором указано начало отсчета О и единица масштаба (рис. 3.39).
, на котором указано начало отсчета О и единица масштаба (рис. 3.39).
 M(ρ, φ) Y M
M(ρ, φ) Y M
ρ ρ
y
0 φ ρ 0 φ x
1 x
Рис. 3.39 Рис. 3.40
При этом луч 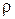 называется полярной осью, а точка О – полюсом. Положение точки M плоскости можно определить парой чисел
называется полярной осью, а точка О – полюсом. Положение точки M плоскости можно определить парой чисел 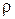 и
и 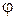 , где
, где 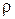 - длина радиуса-вектора точки М, то есть
- длина радиуса-вектора точки М, то есть 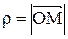 , а
, а 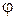 - угол между осью
- угол между осью 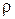 и радиусом-вектором точки М. Таким образом,
и радиусом-вектором точки М. Таким образом, 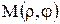 . Числа r, j называются полярными координатами точки М.
. Числа r, j называются полярными координатами точки М.
Если декартову систему XOY совместить с полярной так, как на рис. 3.40, то нетрудно видеть, что 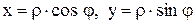 .
.
Итак, связь между декартовыми координатами x, y точки М и ее полярными координатами r, j выражается формулами
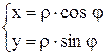 (1), где
(1), где  или
или 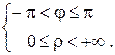
Решив уравнение (1) относительно r и j, получим формулы перехода от декартовых координат x, y к полярным координатам r, j
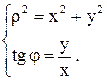 (2)
(2)
Из последних формул видно, что при переходе от декартовых координат к полярным выражение 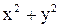 заменяется значительно более простым:
заменяется значительно более простым: 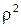 . Этим обстоятельством объясняется преимущество полярной системы координат перед декартовой во многих случаях: уравнение кривой в полярной системе зачастую принимает более простой вид. Приведем примеры.
. Этим обстоятельством объясняется преимущество полярной системы координат перед декартовой во многих случаях: уравнение кривой в полярной системе зачастую принимает более простой вид. Приведем примеры.
Пример. Записать уравнение следующих кривых в полярных координатах и построить эти кривые:
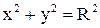 ,
, 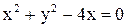 ,
,  ,
,  .
.
Уравнению 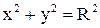 соответствует окружность (рис. 3.41).
соответствует окружность (рис. 3.41).
 Y
Y
-R 0 R x(ρ) 0 1 4 ρ
Рис. 3.41 Рис. 3.42
Так как 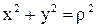 , то
, то 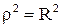 или
или 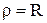 - уравнение этой окружности в полярных координатах.
- уравнение этой окружности в полярных координатах.
Полагая 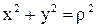 и
и 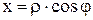 , запишем уравнение окружности
, запишем уравнение окружности 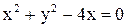 в виде
в виде 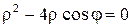 или
или 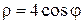 . Окружность
. Окружность 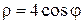 строим по точкам (рис.3.42), полагая, что
строим по точкам (рис.3.42), полагая, что 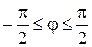 . Для этого составим таблицу значений
. Для этого составим таблицу значений 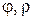 .
.
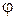
| 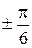
| 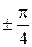
| 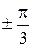
| 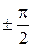
| |
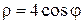
| 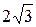
|  
|
Полагая 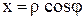 ,
, 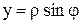 , из уравнения
, из уравнения  получаем
получаем 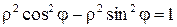 ,
, 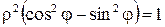 ,
,  ,
,  .
.
Таким образом, полярное уравнение равнобочной гиперболы  имеет вид
имеет вид
 . Область определения этой функции найдем из условия
. Область определения этой функции найдем из условия 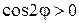 , то есть
, то есть 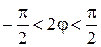 или
или 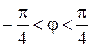 .
.
Составим таблицу значений
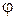
| 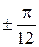
| 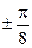
| 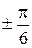
| |
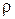
| 1, 1 | 1, 25 | 1, 4 |
Кривая изображена на рис. 3.43.
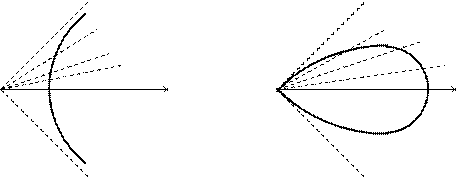 |
0 1 ρ 0 a ρ
Рис. 3.43 Рис. 3.44
Так как 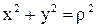 и
и 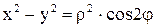 , то из уравнения
, то из уравнения  имеем
имеем 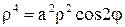 или
или 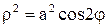 .
.
Таким образом, 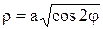 , a > 0. Эта кривая называется лемнискатой Бернулли. Здесь
, a > 0. Эта кривая называется лемнискатой Бернулли. Здесь 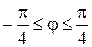 . Составим таблицу значений и построим кривую
. Составим таблицу значений и построим кривую
(рис. 3.44).
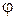
| 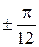
| 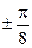
| 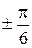
| 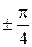
| |
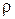
| а | 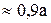
| 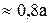
| 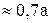
|
Обобщенная полярная система координат.
В полярной системе координат кривая L задается уравнением r=f(j), где r принимает неотрицательные значения, то есть 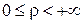 . Это ограничение не позволяет построить кривую L полностью. Причина здесь в следующем.
. Это ограничение не позволяет построить кривую L полностью. Причина здесь в следующем.
В декартовой системе координат XOY кривая L задается уравнением F(x, y)=0 с двумя переменными. Это уравнение может порождать две функции 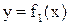 и
и
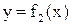 .
.
Примеры. Уравнению  соответствует окружность с центром в точке
соответствует окружность с центром в точке
О(0, 0) и радиусом R=1. Решив его относительно Y, получим 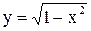 и
и 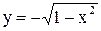 . Графиком первой функции является верхняя, а второй функции – нижняя полуокружности.
. Графиком первой функции является верхняя, а второй функции – нижняя полуокружности.
Аналогично, уравнение равнобочной гиперболы  порождает пару функций
порождает пару функций 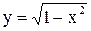 и
и 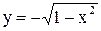 , графиками которых являются соответственно верхние и нижние полуветви гиперболы.
, графиками которых являются соответственно верхние и нижние полуветви гиперболы.
Подобная ситуация возможна и в тех случаях, когда кривая L задана уравнением r=f(j) в полярной системе координат. Чтобы построить кривую L полностью, необходимо допустить, чтобы r принимало отрицательные значения. Таким образом мы приходим к обобщенной полярной системе координат, в которой 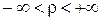 и
и 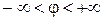 .
.
Примеры. Ранее мы получили для равнобочной гиперболы  ее уравнение в полярной системе
ее уравнение в полярной системе 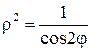 . Отсюда следует, что
. Отсюда следует, что  и
и
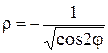 . Графиком второй функции будет левая ветвь гиперболы.
. Графиком второй функции будет левая ветвь гиперболы.
Для лемнискаты Бернулли 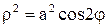 имеем
имеем 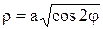 и
и 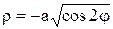
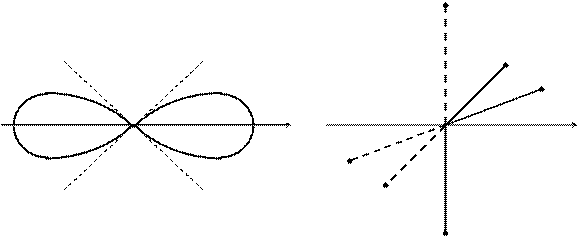
(здесь a > 0). Графиком второй функции будет левая часть “восьмерки” (рис. 3.45).
 B2
B2
A1
M1
-a 0 a ρ 0 ρ
M2
A2
B1
Рис. 3.45 Рис. 3.46
Замечание. В обобщенной полярной системе точки 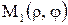 и
и 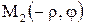 симметричны относительно полюса О (рис. 3.46).
симметричны относительно полюса О (рис. 3.46).
Пример. Построить точки 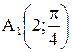 и
и 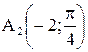 ;
; 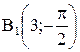 и
и 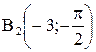 (рис. 3.46).
(рис. 3.46).
Схема построения кривых в обобщенной полярной системе координат.
1. Уравнение кривой F(x, y)=0 записать в полярных координатах, полагая 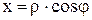 ,
, 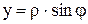 ,
, 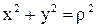 .
.
2. Получив уравнение 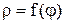 , надо найти область изменения аргумента j и функции r.
, надо найти область изменения аргумента j и функции r.
3. Составить таблицу значений r и j. При этом рекомендуется изменение аргумента j проводить с постоянным шагом h, например 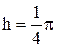 или
или 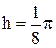 и т.д.
и т.д.
3. Построить полученные точки и соединить их плавной кривой.
Пример. Построить кривую, заданную уравнением:
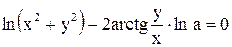 , a > 0.
, a > 0.
Из формул перехода 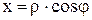 ,
, 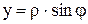 следует, что
следует, что 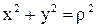 и
и 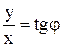 . Подставив эти значения в уравнение кривой, получим
. Подставив эти значения в уравнение кривой, получим 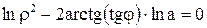 или
или 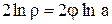 ,
, 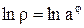 .
.
Таким образом, уравнение кривой в полярной системе координат имеет вид 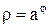 , где a > 0. Эта кривая называется гиперболической спиралью. Здесь
, где a > 0. Эта кривая называется гиперболической спиралью. Здесь 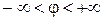 и
и 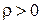 .
.
Составим таблицу значений, полагая здесь a = 2, 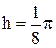 .
.
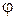
| 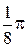
| 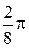
| 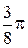
| 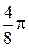
| 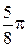
| 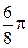
| 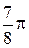
| 
| |
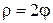
| 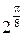
| 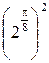
| 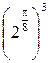
| 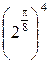
| 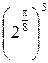
| 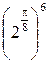
| 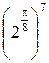
| 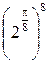
|
Так как 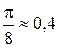 и
и 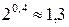 , то получим новую таблицу
, то получим новую таблицу
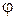
| 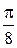
| 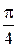
| 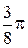
| 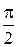
| 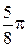
| 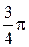
| 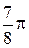
| 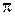
| |
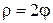
| 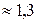
| 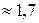
| 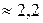
| 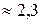
| 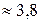
| 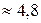
| 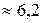
| 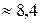
|
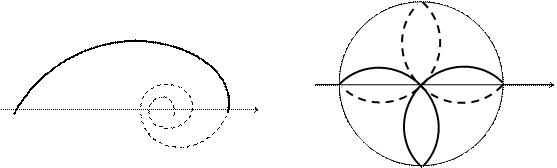
Для построения кривой делим плоскость на секторы с углами 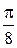 и на полученных лучах откладываем последовательно значения r. Кривая изображена на рис. 3.47.
и на полученных лучах откладываем последовательно значения r. Кривая изображена на рис. 3.47.
0 a ρ
0 1 ρ
Рис. 3.47 Рис. 3.48
Из уравнения 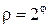 видно, что если
видно, что если 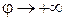 , то
, то 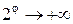 , то есть спираль развертывается против часовой стрелки. Если же
, то есть спираль развертывается против часовой стрелки. Если же 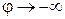 , то
, то 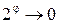 , то есть спираль закручивается по часовой стрелке, делая около полюса О бесконечное число оборотов и не достигая его. Эта часть кривой изображена пунктирно.
, то есть спираль закручивается по часовой стрелке, делая около полюса О бесконечное число оборотов и не достигая его. Эта часть кривой изображена пунктирно.
Пример. Семейство кривых, описываемых в полярных координатах уравнением 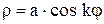 , где a и k – константы, называется розами.
, где a и k – константы, называется розами.
Так как 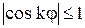 , то из уравнения розы следует, что вся кривая умещается внутри круга радиуса а. Количество лепестков розы зависит от k: при k – четном роза содержит 2k лепестков, при k – нечетном их будет ровно k.
, то из уравнения розы следует, что вся кривая умещается внутри круга радиуса а. Количество лепестков розы зависит от k: при k – четном роза содержит 2k лепестков, при k – нечетном их будет ровно k.
Построим розу, заданную уравнением  с шагом
с шагом 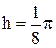 . Здесь k=2, следовательно, роза содержит четыре лепестка. Составим таблицу значений, полагая, что
. Здесь k=2, следовательно, роза содержит четыре лепестка. Составим таблицу значений, полагая, что 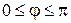 .
.
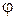
| 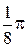
| 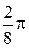
| 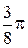
| 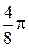
| 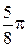
| 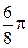
| 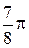
| 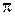
| |
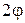
| 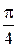
| 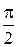
| 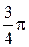
| 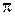
| 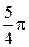
| 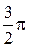
| 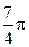
| 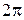
| |
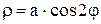
| a | 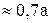
| 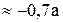
| -a | 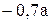
| 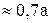
| a |
Кривая изображена на рис. 3.48. Часть кривой, соответствующая 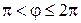 , изображена пунктирно.
, изображена пунктирно.