
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Возможности построения графиков в прямоугольных координатах в пакете Mathcad
|
|
Определим рассматриваемую функцию (например, (5)) с предварительным определением всех численных значений входящих констант с помощью оператора инициализации: =. Построения графика без численного определения параметров невозможно.
На математической панели выберем символ графики.
На листе появятся два прямоугольника, вдоль левой вертикальной и нижней горизонтальной сторон внутреннего прямоугольника будут фигурировать по три метки: одна в середине и две по краям. Серединные метки предназначены для определения значений аргументов по осям: по горизонтали это 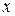 , а по вертикали
, а по вертикали 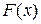 . Затем увести мышку с области графика и щелкнуть мышкой вне области графика. Появится график функции, причем по умолчанию интервал по оси
. Затем увести мышку с области графика и щелкнуть мышкой вне области графика. Появится график функции, причем по умолчанию интервал по оси 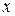 будет выбран от -10 до +10. В дальнейшем масштабы могут меняться произвольно по горизонтальной и вертикальной осям.
будет выбран от -10 до +10. В дальнейшем масштабы могут меняться произвольно по горизонтальной и вертикальной осям.
Если мы хотим на этом же графике построить еще одну функцию, то ее можно ввести после 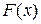 через запятую. Если вводимая функция относится к классу встроенных функций в пакете Mathcad (справку по ним можно получить с помощью меню Вставка/Функции/ с последующим выбором из выпадающего списка), то эту функцию можно ввести без предварительного определения. Например, функцию
через запятую. Если вводимая функция относится к классу встроенных функций в пакете Mathcad (справку по ним можно получить с помощью меню Вставка/Функции/ с последующим выбором из выпадающего списка), то эту функцию можно ввести без предварительного определения. Например, функцию 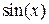 .
.
Подобное представление на одном графике одновременно двух функций позволяет примерно представить себе количество действительных корней сложных уравнений и даже дать предварительную оценку их величин.
Домашнее задание после 1 семинара.
В качестве домашнего задания предлагается вспомнить все сведения из линейной алгебры относительно возможного решения систему двух линейных уравнений с двумя неизвестными. Нарисовать на плоскости две прямые соответствующие этим уравнениям.
Проиллюстрировать графически три возможности, когда система: имеет единственное решение, не имеет решение (две параллельные прямые), имеет бесконечное множество решений (прямые сливаются). Попробовать воспользоваться для иллюстрации графическими возможностями пакета Mathcad.
|