Решение заданий

Задачи

Решение заданий

Исследуя, решая и анализируя задания ГИА, мною было выделено несколько групп планиметрических задач по теме «Треугольник».

ü Задачи, на нахождение синуса, косинуса, тангенса острого угла прямоугольного треугольника

1.В треугольнике ABC угол C равен 90^о, AB = 10, AC = 8.Найдите cos B.

Решение.

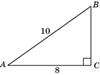
В прямоугольном Δ ABC по теореме Пифагора BC = 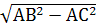=6.

Следовательно, cos B= 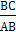= 0, 6.

Ответ: 0, 6.

2. В треугольнике ABC угол C равен 90^о, высота CH= 6, AC = 10. Найдите tgA.

Решение.

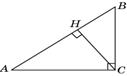
В прямоугольном Δ ACH по теореме Пифагора AH = 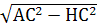=8.

Следовательно, tg A = = 0, 75.

Ответ. 0, 75.

ü Задачи, на нахождение сторон прямоугольного треугольника

1.В Δ ABC угол C = 90^о, tgA = 0, 75, AC = 8. Найдите AB.

Решение.

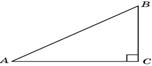
Так как tgA = 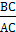, то 0, 75 = .

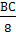Имеем ВС=8∙ 0, 75=6.

По теореме Пифагора находим AB = 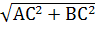= 10.

Ответ: 10

ü Задачи, на нахождение высоты прямоугольного треугольника, проведённой из вершины прямого угла

1. В Δ ABC угол C равен 90^о, CH – высота, BC = 6, cosA = 0, 8. Найдите CH.

Решение.

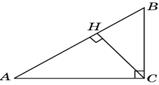
Так как ВС=6, и cos А = 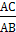= 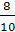, следовательно АС=8, АВ=10. По свойству АС= , тогда 8= 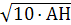, значит АН=6, 4. По теореме Пифагора СН= 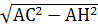=4, 8.

Ответ: 4, 8.

ü Задачи, на нахождение элементов равнобедренного треугольника

1. В Δ ABC AC = BC = 10, sin В = 0, 8. Найдите AB.

Решение.

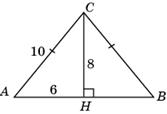
Проведем высоту CH. Так как sin В = 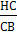. Имеем CH = ВC ∙ sin В = 10∙ 0, 8=8. По теореме Пифагора находим ВH = 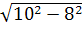= 6. Так как Δ АВС равнобедренный, то АН=НВ и, следовательно, AB = 12

Ответ: 12.

2. ВΔ ABCAC = BC, AB = 10, cosA = 0, 6. Найдите высоту AH.

Решение.

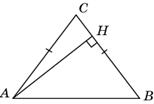
В равнобедренном Δ ABC угол A равен углу B, следовательно cosA=cosВ=, тогда BH = AB ∙ cos B = =10∙ 0, 6= 6. По теореме Пифагора находим AH= 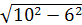= 8.

Ответ: 8.

3. В Δ ABC AB = BC, высота CH равна 5, tgC = 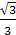. Найдите AC.

Решение.

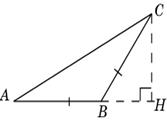
В равнобедренном Δ ABC угол A равен углу C, значит tg С= tg А= 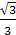= 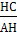, тогда АН= 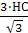= = 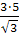5 .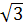

По теореме Пифагора находим AC= 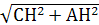= 10.

Ответ: 10.

4. В Δ ABCAC = BC, AB = 10, высота AH равна 8. Найдите cosA.

Решение.

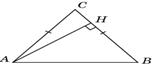
В прямоугольном Δ ABH по теореме Пифагора находим BH= 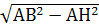= 6, следовательно

cos B = 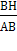=0, 6. Так как АС=ВС, то Δ ABС- равнобедренный, угол А равен углу В и, следовательно, cos A = cos B = 0, 6.

Ответ: 0, 6.

5. В Δ ABCAB = BC, высота CH = 6, AC= 10. Найдите тангенс угла ACB.

Решение.

По теореме Пифагора в прямоугольном Δ ACH, AH = 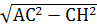= 8. Откуда tg A = 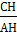= 0, 75. Так как ∟ A =∟ C Δ ABC, то

tg∟ ACB= tg A= 0, 75.

Ответ: 0, 75

ü Задачи на внешний угол треугольника

1.В Δ ABC угол C равен 90^о, AB = 10, BC = 6. Найдите синус внешнего угла при вершине A.

Решение.

Д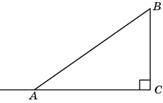

Так как ∟ ДАВ= 180 º - ∟ ВАС, то sin ∟ ДАВ= sin (180 º - ∟ ВАС) =

=sin ∟ ВАС=0, 6.

Ответ: 0, 6.

ü Задачи, на нахождение угла между медианой и высотой, биссектрисой и высотой, медианой и биссектрисой, проведённых из вершины прямого угла

1. Острые углы прямоугольного треугольника равны 51º и 39º.Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Решение.

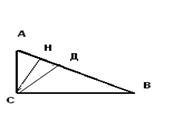
По свойству ∟ А=51°, а СН – высота, то ∟ АСН=90°-51°=39°.Так как СД -биссектриса, то ∟ АСД=∟ ДСВ=∟ АСВ: 2=90°: 2=45°. Следовательно ∟ НСД=∟ АСД-∟ АСН=45°-39°=6°.

Ответ: 6.

2. Острые углы прямоугольного треугольника равны 53 и 37°.Найдите угол между медианой и высотой, проведенными из вершины прямого угла. Ответ дайте в градусах. Решение.

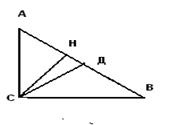
Так как СН высота, то ∟ АСН=90°-∟ А=90°-53°=37°. Поскольку ∟ АСВ=90°, то∟ НСВ=90°-∟ АСН=53°. По свойству медианы прямоугольного треугольника СД=ДВ, следовательно, ∟ ДСВ=∟ ДВС=37°, отсюда ∟ НСД=53°-37°=16°

Ответ: 16.