Теплопроводность плоского тела

СТАЦИОНАРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ

Теплопроводность плоского тела

Однослойное плоское тело. Начнем рассмотрение задачи о распределении температуры в теле (среде) при стационарном режиме с аналитического метода.

Условимся под однослойным плоским телом понимать всякое тело, имеющее ограниченные размеры по высоте (тело, имеющее толщину) и неограниченные размеры по двум другим направлениям (в плане). Такое тело носит название пластины. В наших задачах в качестве однослойного плоского тела могут быть приняты ледяной или снежный покров, слой почвогрунта или воды, стенки гражданских и промышленных сооружений.

Рассмотрим плоское тело толщиной δ, направление которой совпадает с осью z декартовой системы координат, и неограниченного протяжения по направлению двух других осей х и у.

Пусть на поверхностях тела поддерживается постоянной температура t ₁ и t ₂ (стационарная задача).

При стационарном тепловом режиме температура тела во времени остается постоянной. Поэтому в дифференциальном уравнении теплопроводности без источников и стоков теплоты (3.52), позволяющем определить температуру в зависимости от времени и координат в любой точке поля, производная ∂ t/∂ τ =0. В связи с этим обстоятельством, а также ввиду того, что рассматривается одномерная задача, температура изучаемого тела будет функцией только одной координаты. Поэтому уравнение (3.52) запишется в виде уравнения (3.61):

d ² t / dz ² = 0. (4.1)

Интегрирование этого уравнения приводит к следующим решениям:

dt/dz = C ₁; dt = C ₁ dz, (4.2)

t = C ₁ z + C ₂, (4.3)

где C ₁ и C ₂ — постоянные интегрирования, которые могут быть определены при граничных условиях первого рода, названных выше, т. е.:

1) при z = 0 t = t ₁,

2) при z = δ t = t ₂. (4.4)

Из уравнения (4.3) видно, что распределение температуры по координате z подчиняется закону прямой. Если это распределение изучается в ледяном покрове, то t ₁ < t ₂. Тепловой поток в этом случае направлен снизу вверх.

Подставив первое граничное условие из системы (4.4) в уравнение (4.3), получим

C ₂ = t ₁, (4.5)

а, подставив второе, с учетом равенства (4.5)

t ₂ = C ₁δ + t ₁, (4.6)

откуда

C ₁ = (t ₂ - t ₁)/ δ. (4.7)

С учетом постоянных интегрирования C ₁ и C ₂ уравнение (4.3), представляющее собою прямую, примет вид

t = t ₁ + z (t ₂ - t ₁)/ δ. (4.8)

Уравнение (4.8) определяет распределение температуры по толщине однослойного плоского тела.

При втором граничном условии (4.4) уравнение (4.8) можно представить в виде равенства

(t ₂ - t ₁)/ δ = (t ₂ - t ₁)/ δ, (4.9)

из которого, заменив левую часть по закону Фурье (3.9), получим

q /λ = - (t ₂ - t ₁)/ δ = (t ₂ - t ₁)/ δ (4.10)

или удельный расход теплоты через однослойное плоское тело

q = λ (t ₁ - t ₂)/ δ. (4.11)

Многослойное плоское тело. Рассмотрим теперь плоское тело, состоящее из n слоев толщиной δ ₁, δ ₂,..., δ _n и с коэффициентами теплопроводности λ ₁, λ ₂,..., λ _n. Слои тела плотно прижаты друг к другу. Прообразом такого многослойного плоского тела (многослойной стенки или толщи) может выступать, например, снежно-ледяной покров (рис.4.1.). При граничных условиях первого рода должна быть задана температура на поверхностях многослойного тела: на поверхности снега — t ₁ и на нижней поверхности льда — t _n+1. Задачей в этом случае является установление температуры на границах каждого слоя и расхода теплоты через всю многослойную толщу. При трехслойной толще, как в нашем примере, должна быть задана температура t ₁ и t ₄, а отыскивается t ₂ и t ₃.

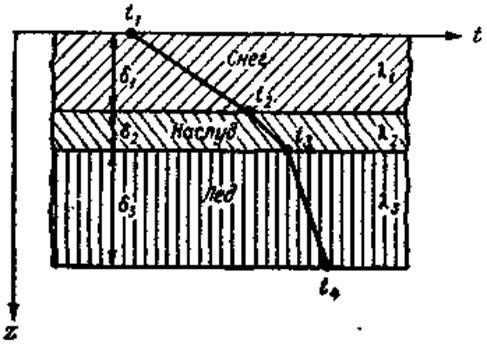
Рис. 4.1. Теплопроводность многослойной толщи при граничных условиях первого рода [8]

Если в слоях толщи нет источников и стоков теплоты, то, по закону сохранения энергии, теплота, вошедшая в первый слой, должна пройти все слои толщи без ее увеличения и потерь.

Для решения поставленной задачи нет необходимости возвращаться к общему уравнению теплопроводности при стационарном режиме (4.1). Для этого достаточно воспользоваться решением (4.11). Согласно уравнению (4.11), для каждого слоя толщи, состоящей из n слоев, можно записать:

q = (λ ₁/δ ₁) (t ₁ - t ₂),

q = (λ ₂/δ ₂) (t ₂ - t ₃),

…………………….

q = (λ _n/δ _n) (t _n - t _n+1). (4.12)

Перепишем систему уравнений (4.12) относительно разности значений температуры в каждом слое:

t ₁ - t ₂ = q δ ₁/λ ₁,

t ₂ - t ₃ = q δ ₂/λ ₂,

……………..

t _n - t _n+1 = q δ _n/λ _n. (4.13)

Складывая почленно левые и правые части системы (4.13) получаем

t ₁ - t _n+1 = q (δ ₁/λ ₁ + δ ₂/λ ₂ + … + δ _n/λ _n). (4.14)

Из этой формулы определим выражение для удельного теплового потока многослойного плоского тела:

q = (t ₁ - t _n+1)/(δ ₁/λ ₁ + δ ₂/λ ₂ + … + δ _n/λ _n). (4.15)

Это выражение было получено нами ранее при рассмотрении коэффициента теплопередачи в виде

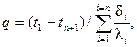
(4.16)

где i — номер слоя.

Решая уравнение (4.14) относительно температуры t _n+1, получаем

t _n+1 = t ₁ - q (δ ₁/λ ₁ + δ ₂/λ ₂ + … + δ _n/λ _n). (4.17)

Внутри слоя температуру необходимо считать по формуле (4.8).

Используя выражение (4.17), можно найти температуру на границе между интересующими нас слоями толщи. В данном случае под индексом n необходимо подразумевать номер i -го слоя толщи, для внутренней границы которой отыскивается температура. Например, температура на границе между первым и вторым слоями толщи

t ₂ = t ₁ - q (δ ₁/λ ₁), (4.18)

а между вторым и третьим

t ₃ = t ₁ - q (δ ₁/λ ₁ + δ ₂/λ ₂). (4.19)

Здесь в первом случае n + 1 = 2, а во втором случае n + 1 = 3

Удельный тепловой поток q определяется по выражению (4.15) при заданных граничных условиях первого рода.

Ход температуры внутри многослойной плоской толщи представляет собой ломаную линию. Внутри каждого слоя температура изменяется по прямой, согласно уравнению

t_{i , z} = t_i - q(z_i /λ _i), (4.20)

где z_i — расстояние внутри рассматриваемого i -го слоя от поверхности предыдущего слоя, температура на границе между которыми равна t_i.