Дифференциальное уравнение температурного поля турбулентного потока

ГИДРОТЕРМИЧЕСКИЙ РАСЧЕТ ВОДОЕМОВ И ВОДОТОКОВ

Целый ряд практических задач, выдвигаемых в настоящее время гидрологией и гидротехникой, требуют изучения распространения теплоты в водных ламинарных или турбулентных потоках.

Дифференциальное уравнение температурного поля турбулентного потока

В пределах потока выделим в системе декартовых координат x, у, z элементарный параллелепипед с гранями dx, dy, dz (рис. 5.1). Рассмотрим его тепловой баланс. Через грани параллелепипеда теплота будет распространяться двумя путями:

1) вместе с водными массами, пронизывающими грани параллелепипеда со скоростями υ _x, υ _y, υ _z — молярный перенос;

2) молекулярной теплопроводностью в ламинарных потоках (с коэффициентом теплопроводности λ) и турбулентной теплопроводностью в турбулентных потоках (с коэффициентом теплопроводности λ _т, во много раз превышающим λ).

Рис. 5.1. Схема к выводу дифференциального уравнения теплопроводности потока жидкости [8]

Уравнение теплового баланса для выделенного элементарного объема жидкости в этом случае будет иметь следующий вид:

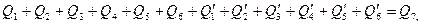
(5.1)

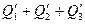
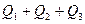где и т. д. — количество теплоты, обусловленное скоростью потока жидкости через соответствующие грани в направлении осей x, у, z завремя d τ, a и т. д. — количество теплоты, обусловленное теплопроводностью потока через эти же грани и за то же время d τ.

В том случае, когда потоки теплоты, проходящие через грани параллелепипеда, взаимно не компенсируются, т. е. в него входит теплоты больше, чем выходит, или наоборот, будет наблюдаться изменение энтальпии рассматриваемого объема dx dy dz, которое в уравнении (5.1) обозначено через Q ₇.

Определим составляющие уравнения (5.1).

Количество теплоты, поступившее в параллелепипед через грань dy dz молярным путем за время d τ, оценим по формуле

Q ₁ = c ρ υ _x t dy dz dτ, (5.2)

где c и ρ — удельная теплоемкость и плотность жидкости; υ _x — проекция скорости на ось x; ρ V_x dy dz — расход жидкости через грань параллелепипеда dy dz; t — температура жидкости, проходящей через грань dy dz.

Количество же теплоты, выходящее из элементарного параллелепипеда через противоположную грань, отстоящую от первой на расстоянии dx,

(5.3)

где ∂ υ _x / ∂ x и ∂ t / ∂ x — изменение скорости и температуры жидкости внутри выделенного объема по оси x. Знак минус в этом уравнении свидетельствует о том, что Q ₂ — уходящее из элементарного параллелепипеда количество теплоты.

Для остальных граней параллелепипеда будем соответственно иметь:

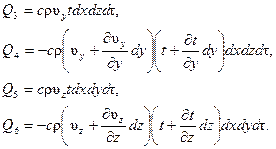
(5.4)

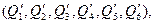Другие шесть слагаемых уравнения (5.1) обусловленные турбулентной теплопроводностью, определим по следующим формулам:

(5.5)

где λ _т = cА _т — коэффициент турбулентной теплопроводности, А _т — коэффициент турбулентного обмена жидкости.

Изменение энтальпии рассматриваемого объема Q ₇ определим по формуле

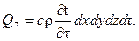(5.6)

Решая совместно уравнения (5.1) — (5.6), получаем

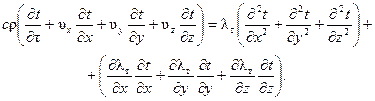
(5.7)

При совместном решении уравнений (5.1) — (5.6) учтено условие неразрывности несжимаемой жидкости

∂ υ _x / ∂ x + ∂ υ _y / ∂ y + ∂ υ _z / ∂ z = 0 (5.8)

и отброшены слагаемые

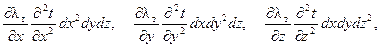
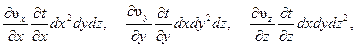а также

из-за их малости по сравнению с другими. Уравнение (5.7) носит название дифференциального уравнения температурного поля турбулентного потока жидкости. Его также называют уравнением энергии.

При постоянном значении коэффициента турбулентной теплопроводности λ _т для всего потока уравнение (5.7) примет вид

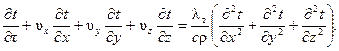(5.9)

Коэффициент турбулентной теплопроводности изменяется в зависимости от координат x, у, z. Но, так как накопленные к настоящему времени знания об его изменений по координатам не позволяют определять характер этой зависимости, его обычно принимают постоянным.

Учитывая, что левая часть уравнения (5.9) — полная производная от температуры по времени, его можно представить в виде

dt/d τ = а _т (∂ ²t/∂ x² + ∂ ²t/∂ y² + ∂ ²tl∂ z²) (5.10)

или

dt/d τ = а _т Ñ ² t, (5.11)

где а _т = λ _т/(c ρ) —коэффициент турбулентной температуропроводности.

При наличии в потоке внутренних источников теплоты (например, теплоты, появляющейся при изменении агрегатного состояния воды — при внутриводной кристаллизации, при переходе кинетической энергии движения потока в тепловую, при проникновении лучистой энергии в воду и т. д.) уравнение (5.10) должно быть дополнено еще одним слагаемым, связанным с источником

(5.12)

где W — интенсивность внутреннего источника (количество теплоты, которое выделяется или поглощается единицей объема жидкости).

Из сопоставления выражений (3.52) и (5.10) следует, что уравнение энергии отличается от дифференциального уравнения теплопроводности полной производной, учитывающей три дополнительных слагаемых, и коэффициентом турбулентной температуропроводности а _т.

Для ламинарного потока уравнение энергии аналогично уравнению (5.11):

dt/d τ = а Ñ ² t, (5.13)

где а = λ /(c ρ) — коэффициент температуропроводности жидкости.

В случае установившегося температурного режима водного потока температура в каждой точке его остается неизменной во времени (∂ t/∂ τ = 0) и меняется лишь по направлениям x, у, z, а уравнение (5.9) принимает следующий вид:

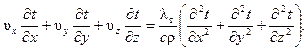(5.14)