
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Символика
|
|
Введение
Общество 21в. – общество информационное. Центр тяжести в решении задач переместился от задач вычислительной математики к задачам на дискретных структурах. Математика нужна не как метод расчета, а как метод мышлению средство формирования и организации…
Такое владение математикой богатой культуры, понимание важности точных формулировок.
В дисциплине мало методов, но много определений и терминов. В основе дискретной математике 4 раздела:
1. Язык дискретной математики;
2. Логические функции и автоматы;
3. Теория алгоритмов;
4. Графы и дискретные экстремальные задачи.
Теория алгоритмов и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.
Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.
Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно сложные задачи (задачи перебора) и неразрешимые задачи.
Мы будем заниматься решением задач реальной размерности с учетом ограниченности временных и емкостных ресурсов ЭВМ.
Множества и операции над ними
Одно из основных понятий математики – множество.
Определение:
Множеством называется совокупность, набор предметов, объектов или элементов.
Множество обозначают: M, N …..
m1, m2, mn – элементы множества.
Символика
A Î M – принадлежность элемента к множеству;
А Ï М – непринадлежность элемента к множеству.
Примеры числовых множеств:
1, 2, 3, … множество натуральных чисел N;
…, -2, -1, 0, 1, 2, … - множество целых чисел Z.
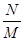 множество рациональных чисел а.
множество рациональных чисел а.
I – множество иррациональных чисел.
R – множество действительных чисел.
K – множество комплексных чисел.
Множество А называется подмножеством В, если всякий элемент А является элементом В.
А Í В – А подмножество В (нестрогое включение)
Множества А и В равны, если их элементы совпадают.
A = B
Если А Í В и А ¹ В то А Ì В (строгое включение).
Множества бывают конечные и бесконечные.
|М| - мощность множества (число его элементов).
Конечное множество имеет конечное количество элементов.
Пустое множество не содержит элементов: M = Æ.
Пример: пустое множество:
1) множество действительных корней уравнения x2+1=0 пустое: M = Æ.
2) множество D, сумма углов которого ¹ 1800 пустое: M = Æ.
Если дано множество Е и множество и мы рассматриваем все его подмножества, то множество Е называется униварсельным.
Пример: Если за Е взять множество книг то его подмножества: художественные книги, книги по математике, физики, физики …
Если универсальное множество состоит из n элементов, то число подмножеств = 2n.
Если 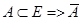 , состоящее из элементов E, не принадлежащих А, называется дополненным.
, состоящее из элементов E, не принадлежащих А, называется дополненным.
Множество можно задать:
1) Списком элементов {a, b, c, d, e};
2) Интервалом 1< x< 5;
3) Порождающей процедурой: xk=pk sinx=0;