Булева алгебра характеристических векторов.

Пусть A < = U, A < - P(U) a - характеристический вектор этого подмножества.

aA = {a, a2..an)

n = [P(U)]

ai = 1, если ai < - A (принадлежит).

ai = 0, если ai не принадлежит A.

U = {1 2 3 4 5 6 7 8 9}

A = {2 4 6 8}

B = {1 2 7}

aA = {0 1 0 1 0 1 0 1 0}

aB = {1 1 0 0 0 0 1 0 0}

или

aA = 010101010 – скобки не нужны

aA= 110000100

Характеристические векторы размерностью n называются булевыми векторами.

Они располагаются в вершинах n – мерного булева куба.

Номером булевого вектора является число в двоичном представлении, которым он является

1101 – номер.

Два булевых вектора называются соседними, если их координаты отличаются только в одном разряде (если они отличаются только одной координатой).

Совокупность всех булевых векторов размерности n называется булевым кубом размерностью Bⁿ.

Булев куб размерности 2

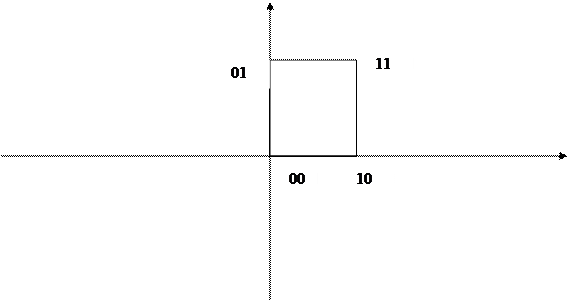
Булев куб размерности 3

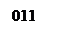0 – нулевой вектор.

Логическое сложение XY	X& Y	X V Y

Отрицание

X = 0 Y = 0

_ _

Х = 1 Y= 1

Для размерности n операции над векторами производятся покоординатно.

Логическая сумма двух векторов – вектор, координаты которого являются логическими суммами соответствующих исходных векторов. Аналогично определено произведение.