Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЗАДАЧА №3. 1) Поток вызовов на АТС – пуассоновский нестационарный с интенсивностью λ(t),зависящей от времени
|
|
1) Поток вызовов на АТС – пуассоновский нестационарный с интенсивностью λ (t), зависящей от времени. На участке времени от 0 час. до 6 час. 40 мин. интенсивность λ (t) возрастает по линейному закону: λ (t) = bt+c, причем к 0 час. она равна 0, 2 вызова в минуту, а в 6 час. 40 минут – 0, 4 вызова в минуту. Найти вероятность того, что за 10 минут от 3 часов 15 минут до 3 часов 25 минут придет не менее трех вызовов.
2) λ 1(t)=0, 2 (вызова/минуту) – к 0 час.
λ 2(t)=0, 4 (вызова/минуту) – к 6 час. 40 мин.
λ 3(t)=? (вызова/минуту) – за 10 минут. от 3 час. 15 мин. до 3 час. 25 мин.
P=? – вероятность прихода 3 вызовов от 3 час. 15 мин. до 3 час. 25 мин.
3) Интенсивность простейшего потока не стационарна и имеет также распределение Пуассона:
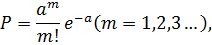

4) λ (t) = bt+c =>
0, 2=b*0+c,
0, 4=b*400+c, от сюда следует b = 0, 0005; c = 0, 2.
λ (t) = 0, 0005*t+0, 2.
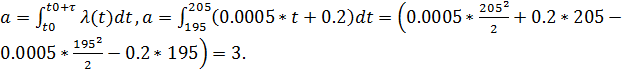
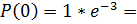 0, 050244916;
0, 050244916;
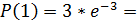 0, 150734749;
0, 150734749;
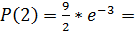 0, 226102123;
0, 226102123;
P(P> =3)=1-0.050244916-0.150734749-0.226102123=0, 572918212.
5) Fortran:
REAL lambda, a, p0, p1, p2, p3
a=3.0
p0 = 1*EXP(-a)
p1 = 3.0*EXP(-a)
p2 = (9.0/2.0)*EXP(-a)
p3 = 1.0-p0-p1-p2
PRINT *, " Task #3"
PRINT *, " p(0) = ", p0
PRINT *, " p(1) = ", p1
PRINT *, " p(2) = ", p2
PRINT *, " P(P> =3) = ", p3