Түріндегі өрнек шексіз.деп аталады 1 страница

$$сандық қ атар

$тізбек

$шегі

$функционал

$$$24 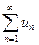қ атарының дербес қ осындылар тізбегінің ақ ырлы.... бар болса, онда берілген тізбек жинақ ты деп аталады.

$$шегі

$реті

$саны

$функциясы

$$$25 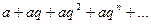геометриялық прогрессия қ атары еселігі 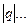болғ анда жинақ ты болады.

$$бірден кіші

$бір

$екі

$ү ш

$$$26 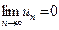шегі бар болса, онда 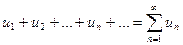қ атары... деп аталады.

$$жинақ ты

$жинақ сыз

$шартты жинақ ты

$абсолют жинақ ты

$$$27 Егер сан қ атары жинақ ты болса, онда оның жалпы мү шесінің шегі....ұ мтылады.

$$нө лге

$бірге

$ү шке

$екіге

$$$28 Егер сан қ атары жинақ ты болса, онда оның дербес қ осындыларының тізбегі....санғ а ұ мтылады.

$$шектелген

$шектелмеген

$бірге

$ү шке

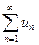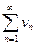$$$29 Егер жә не -оң сандар қ атары мү шелерінекез келге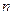н ү шін 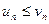тең сіздігі орындалса, онда 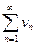қ атарының жинақ тылығ ынан 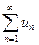қ атарының....болуы шығ ады.

$$жинақ ты

$жинақ сыз

$шартты жинақ ты

$абсолют жинақ ты

$$$30 Егер екі оң сандар қ атарының жалпы мү шелері ү шін 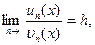мұ ндағ ы 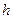нолге тең емес кез келген сан, тең дігі орындалса, онда екеуіде....не жинақ ты, не жинақ сыз болады

$$бірдей

$ә ртү рлі

$шартты

$абсолют

$$$31 Егер 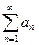оң сандар қ атары ү шін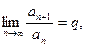 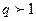, шарты орындалса, онда берілген қ атар....

$$жинақ сыз

$жинақ ты

$абсолют жинақ ты

$шартты жинақ ты

$$$32 Егер 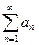- оң сандар қ атары ү шін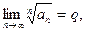 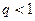, шарты орындалса, онда берілген қ атар...

$$жинақ ты

$абсолют жинақ ты

$шартты

$жинақ сыз

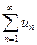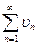$$$33 Егер жә не - оң сандар қ атарларының мү шелеріне кез келген n ү шін 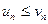тең сіздігі орындалса, онда 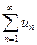қ атарының жинақ сыздығ ынан 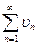қ атарының... болуы шығ ады.

$$жинақ сыз

$жинақ ты

$абсолют жинақ ты

$шартты жинақ ты

$$$34 Егер 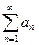-оң сандар қ атары ү шін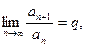 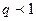шарты орындалса, онда берілген қ атар...

$$жинақ ты

$абсолют жинақ ты

$шартты жинақ ты

$жинақ сыз

$$$35 Егер 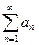-оң сандар қ атары ү шін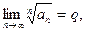 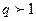шарты орындалса, онда берілген қ атар....

$$жинақ сыз

$жинақ ты

$абсолют жинақ ты

$шартты жинақ ты

$$$36 Таң балары ауыспалы сан қ атары жинақ ты болуы ү шін оның жалпы мү шесінің шегі нолге ұ мтылуы жеткілікті бола ма?

$$жоқ

$жеткілікті

$ә ртү рлі

$жеткілікті

$$$37 Таң балары ауыспалы сан қ атары жинақ ты болуы ү шін оның мү шелерінің абсолют шамаларының кемуі жеткілікті бола ма?

$$жоқ

$жеткілікті

$ә ртү рлі

$жеткілікті

$$$38 Егер 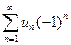-таң балары айнымалы сан қ атары мү шелерінің абсолют шамаларынан қ ұ ралғ ан қ атар жинақ ты болса, онда берілген қ атар...жинақ ты

$$абсолют

$жинақ сыз

$жинақ ты

$шартты

$$$39 Егер 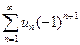- таң балары ауыспалы сан қ атары мү шелерінің абсолют шамаларынан қ ұ ралғ ан қ атар жинақ сыз болса, онда берілген қ атар...жинақ ты.

$$шартты

$абсолют

$жинақ сыз

$жинақ ты

$$$40 Мү шелері х айнымалысының функциясы болатын 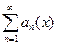тү ріндегі қ атарды... қ атар деп атайды.

$$функционалдық

$сандық

$дә режелік

$тізбек

$$$41 Мү шелері х аргументінің дә режелік функциялары болатын 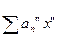немесе 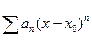тү ріндегі функционалдық қ атарларды.... қ атар деп атайды.

$$дә режелік

$сандық

$тізбек

$тригонометриялық

$$$42 Функцияны 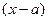дә режесі бойынша дә режелік қ атар тү рінде кө рсету функцияны...қ атарына жіктеу деп атайды.

$$Тейлор

$дә режелік

$сандық

$Маклорен

$$$43 Егер Тейлор қ атарына жіктеу 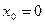нү ктесінің маң айында болса, онда мұ ндай қ атарды.... қ атары деп атайды.

$$Маклорен

$дә режелік

$сандық

$Тейлор

$$$44 Егер 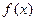-функциясы [- 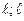] кесіндісінде жұ п функция болса, онда оның Фурье қ атарына жіктелуінде тек.... болады.

$$косинустар

$синустар

$тангенс

$сандар

$$$45 Егер 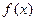- функциясы (- 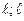) аралығ ында тақ функция болса, онда оның Фурье қ атарына жіктелуінде тек... болады.

$$синустар

$косинус

$тангенс

$сандар

$$$46 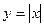функциясының 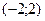аралығ ында Фурье қ атарына жіктелуінде....коэффициенттері нолге тең.

$$b_n

$a_n

$а

$b

$$$47 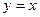функциясының 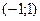аралығ ында Фурье қ атарына жіктелуінде....коэффициенттері нолге тең.

$$a_n

$b_n

$а

$b

$$$48 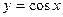функциясының 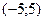аралығ ында Фурье қ атарына жіктелуінде тек....болады.

$$косинус

$синустар

$тангенс

$сандар

$$$49 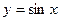функциясының 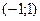аралығ ында Фурье қ атарына жіктелуінде тек....болады.

$$синустар

$косинус

$тангенс

$сандар

$$$50 Есептең із: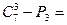

$$29

$-7

$40

$35

$$$51 Есептең із:

$$

$

$

$

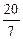
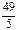
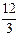
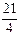
$$$52 Есептең із: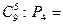

$$

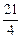
$0, 45

$

$

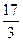
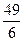
$$$53 Есептең із: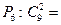

$$20

$15

$49

$

$$$54 Тең деуді шешің із: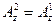

$$2

$3

$45

$0

$$$55 Есептең із: =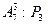

$$35

$20

$10

$0

$$$56 Тең деуді шешің із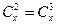

$$5

$6

$7

$0

$$$57 Есептең із: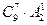

$$72

$14

$48

$15

$$$58 Абонент телефон нө мірінің соң ғ ы екі цифрын ұ мытып қ алды, бірақ олардың ә ртү рлі екенін біледі.Таң дамай кез келген екі цифрды тере салды. Сонда керекті цифрлардың терілуінің ық тималдығ ын табың дар.

$$

$

$

$

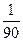
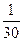
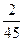
$$$59 Бірдей тө рт қ ағ аздың ә рқ айсысында Я, С, И, А ә ріптерінің біреуі жазылғ ан. Сонда осы ә ріптерді таң дамай АСИЯ сө зінің шығ у ық тималдығ ын табың дар.

$$

$

$

$

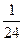
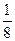
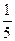
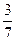
$$$60 Тең гені екі рет лақ тырғ анда екі рет герб тү су ық тималдығ ын табың дар.

$$0, 25

$0, 5

$0, 125

$0

$$$61 Тең гені екі рет лақ тырғ анда екі рет цифр тү су ық тималдығ ын табың дар.

$$0, 25

$0, 5

$0, 125

$0

$$$62 Тең гені екі рет лақ тырғ анда бір рет цифр жағ ы тү су ық тималдығ ын табың дар.

$$0, 5

$0, 25

$0, 125

$0

$$$63 Жә шіктегі 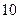деталдың екеуі жарамсыз. Таң дамай алынғ ан ү ш деталдың ү шеуі де жарамды болу ық тималдығ ын табың дар.

$$

$

$

$

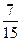
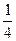
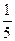
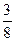
$$$64 Жә шіктегі 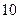деталдың екеуі жарамсыз. Таң дамай жә шіктен алынғ ан ү ш деталдың екеуі жарамсыз болу ық тималдығ ын табың дар.

$$

$

$

$

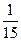
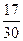
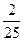
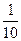
$$$65 Жә шіктегі 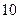деталдың екеуі жарамсыз. Таң дамай алынғ ан ү ш деталдың біреуі жарамсыз болу ық тималдығ ын табың дар.

$$

$

$

$

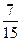
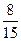
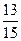
$$$66 Абонент телефон нө мірінің соң ғ ы цифрын ұ мытып қ алды да, таң дамай тере салды. Сонда керекті цифрдың терілуінің ық тималдығ ын табың дар.

$$0, 1

$0, 2

$0, 25

$0, 125

$$$67 Қ орапта 6 қ ара, 3 ақ шарлар бар. Қ ораптан алынғ ан 4 шардың екеуі ақ шар болуы ық тималдығ ын табың дар.

$$

$

$

$

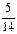
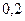
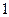
$$$68 Қ орапта 6 қ ара, 3 ақ шарлар бар. Қ ораптан таң дамай бірінші алынғ ан шардың қ айтадан қ орапқ а салынбайды/ ақ болу, екінші алынғ ан шардың қ ара болу ық тималдығ ын табың дар.

$$

$

$

$

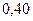
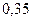
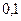
$$$69 Қ орапта 6 қ ара, 3 ақ шарлар бар. Қ ораптан таң дамай бірінші алынғ ан шардың (қ айтадан қ орапқ а салынбайды) қ ара болу, екінші алынғ ан шардың ақ болу ық тималдығ ын табың дар.

$$

$

$

$

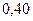
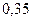
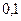
$$$70 Абонент телефон нө мірінің соң ғ ы ү ш цифрын ұ мытып қ алды да, осы ү ш цифрдың ә ртү рлі екендігін есте сақ тай отырып, таң дамай тере салды. Сонда керекті цифрлардың терілуінің ық тималдығ ын табың дар.

$$

$

$

$

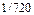
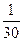
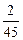
$$$71 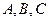оқ иғ алары толық топ қ ұ рады жә не 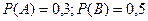. Табу керек: .

$$

$

$

$

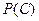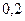
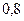
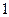
$$$72 Екі тә уелсіз оқ иғ алардың ә рқ айсысының пайда болу ық тималдық тары сә йкес 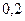жә не 0, 8-ге тең. Тек бір ғ ана оқ иғ аның пайда болу ық тималдығ ын табың дар.

$$

$

$

$

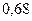
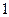
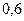
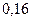
$$$73 Екі тә уелсіз оқ иғ алардың ә рқ айсысының пайда болу ық тималдық тары сә йкес 0, 2 жә не 0, 8-ге тең. Ең болмағ анда бір оқ иғ аның пайда болу ық тималдығ ын табың дар.

$$0, 84

$0, 1

$0, 6

$0, 16

$$$74 Табу керек: М(Х + У), егер М(Х)=4 и М(У)=7

$$11

$3

$25

$0

$$$75 Х кездейсоқ шамасы келесі ү лестірім заң ымен берілген:

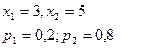Табу керек: М(х)

$$4, 6

$4

$5

$0, 5

$$$76 Х кездейсоқ шамасы келесі ү лестірім заң ымен берілген:

Табу керек: М(x)

$$3, 7

$0, 40

$2, 20

$2, 21

$$$77 Х кездейсоқ шамасы келесі ү лестірім заң ымен берілген:

Табу керек:

$$0, 16

$0, 40

$2, 20

$2, 21

$$$78 Х кездейсоқ шамасы келесі ү лестірім заң ымен берілген:

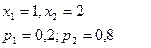Табу керек: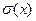

$$0, 40

$0, 45

$2, 20

$2, 21

$$$79 Х, У кездейсоқ шамалары келесі ү лестірім заң ымен берілген:

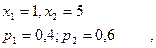
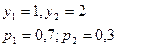Табу керек: М(х+у)

$$4, 7

$5

$7

$8, 3

$$$80 n тә жирибе жасағ анда оқ иғ аның к рет пайда болу ық тималдығ ын анық тайтын Бернулли формуласын кө рсетің дер:

$$

$

$

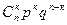
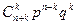
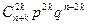
$ дұ рыс жауабы жоқ

$$$81 Дискретті кездейсоқ шаманың математикалық ү міті 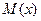қ андай формуламен есептеледі?

$$

$

$

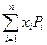
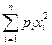
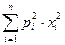
$дұ рыс жауабы жоқ

$$$82 Х кездейсоқ шаманың дисперсиясы қ андай формуламен табылады?

$$

$

$

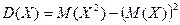
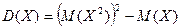
$ D(X)= 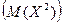- M(X)

$$$83 Ү лестірім заң ымен белілген Х дискретті кездейсоқ шаманың математикалық ү мітін табындар

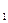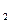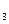x =-1, x =2, x =4

p 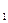=0, 4, p 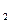=0, 5, p 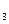=0, 1

$$

$

$

$

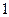
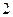
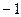
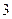
$$$84 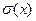орта квадраттық ауытқ уды қ андай формуламен табады:

$$

$

$

$

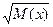
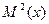
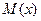
$$$85 Ү лестірім заң ымен берілген Х дискретті кездейсоқ шаманың дисперсиясын табың дар:

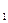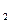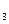x =-1, x =2, x =4

p 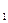=0, 4, p 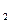=0, 5, p 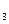=0, 1

$$

$

$

$

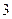
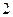
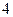
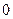
$$$86 Ү лестірім заң ымен берілген Х дискретті кездейсоқ шаманың орта квадраттық ауытқ уын табың дар:

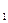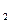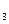x =-1, x =2, x =4

p 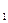=0, 4, p 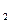=0, 5, p 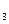=0, 1

$$

$

$

$

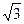
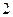
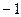
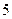
$$$87 Екі тә уелсіз оқ иғ аның қ осындысының ық тималдығ ы олардың ық тималдық тарының

$$қ осындысына тең

$айырмасына тең

$кө бейтіндісіне тең

$бө ліндісіне тең

$$$88 Ық тималдығ ы бірге тең болатын оқ иғ аны … оқ иғ а деп атайды.

$$ақ иқ ат

$ақ иқ ат емес

$кездейсоқ

$дискретті

$$$89 Ық тималдығ ы нө лге тең оқ иғ аны … оқ иғ а деп атайды

$$мү мкін емес

$ақ иқ ат

$кездейсоқ

$дискретті

$$$90 Ық тималдығ ы 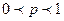ық тималдығ ы аралығ ында болатын оқ иғ аны …. оқ иғ а деп атайды.

$$кездейсоқ

$мү мкін емес

$ақ иқ ат

$дискретті

$$$91Толық топты оқ иғ алардың қ осындысының ық тималдығ ы … тең

$$1

$2

$0

$3

$$$92 Тә уелсіз оқ иғ алардың кө бейтіндісінің ық тималдығ ы олардың ық тималдық тарының

$$кө бейтіндісіне тең

$айырмасына тең

$қ осындысына тең

$бө ліндісіне тең

$$$93 Қ арама –қ арсы оқ иғ алардың ық тималдық тарының қ осындысы 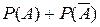тең.

$$1

$2

$0

$3

$$$94 Тә жірибені қ айталау саны - n ө те ү лкен, ал ә рбір тә жірибедегі А оқ иғ асының ық тималдығ ы, р- ө те кіші болғ анда, n рет тә жирибе жү ргізгенде А оқ иғ асының m рет пайда болу ық тималдығ ы … формуласымен табылады

$$Пуассон

$Бернулли

$Гаусс

$Лаплас

$$$95 Егер тә жирибені қ айталағ анда n мен m сандары ү лкен болмаса, онда n рет тә жирибе жү ргізгенде оқ иғ аның m рет пайда болу ық тималдығ ы ….. формуласымен табылады.