Түріндегі өрнек шексіз.деп аталады 4 страница

$

$

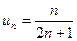
$$$235 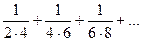.қ атарының жалпы мү шесін жазың ыз:

$$

$

$

$

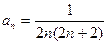
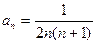
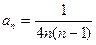
$$$236 Коэффициенттері тұ рақ ты біртекті сызық ты дифференциалдық тең деуінің 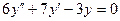сипаттамалық тең деуі:

$$

$

$

$

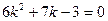
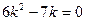
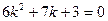
$$$237 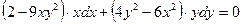тең деуі.... дифференциалдық тең деу болып табылады.

$$толық дифференциалды

$белгісіз функцияғ а қ арағ анда сызық ты

$айнымалылары ажыратылатын

$Бернулли

$$$238 Коэффициенттері тұ рақ ты біртекті сызық ты дифференциалдық тең деуінің 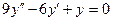сипаттамалық тең деуі:

$$

$

$

$

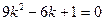
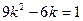
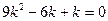
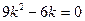
$$$239 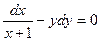дифференциалдық тең деуінің жалпы интегралы немесе жалпы шешімі:

$$

$

$

$

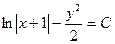
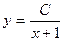
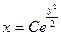
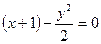
$$$240 y´ ´ -2y´ +2y=0 дифференциалдық тең деуінің шешімі:

$$

$

$

$

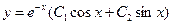
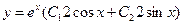
$$$241 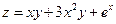функциясының (1; 0) нү ктесіндегі у бойынша дербес туындысын табың ыз.

$$4

$1

$-1

$e

$$$242 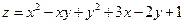функциясының (1; 1) нү ктесіндегі у бойынша дербес туындысын табың ыз

$$ -1

$1

$0

$2

$$$243 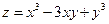функциясының (0; 1) нү ктесіндегі у бойынша дербес туындысын табың ыз.

$$3

$-1

$2

$1

$$$244 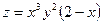функциясының (-1; 0) нү ктесіндегі у бойынша дербес туындысын табың ыз 0

$$0

$-1

$2

$1

$$$245 1-ретті дифференциалдық тең деу деп....айтады.

$$тә уелсіз айнымалыны, ізделінді функцияны жә не туындыны байланыстыратын тең деуді

$бір ө лшемді функцияны байланыстыратын тең деуді

$ізделінді функцияны жә не туындыны байланыстыратын тең деуді

$ізделінді функцияны жә не екінші ретті туындыны байланыстыратын тең деуді

$$$246 1-ретті біртекті дифференциалдық тең деу деп....айтады

$$ноль ө лшемді біртекті функцияларды байланыстыратын тең деуді

$ізделінді функцияны жә не туындыны байланыстыратын тең деуді

$ізделінді функцияны жә не екінші ретті туындыны байланыстыратын тең деуді

$тә уелсіз айнымалыны, ізделінді функцияны жә не туындыны байланыстыратын тең деуді

$$$247 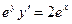дифференциалдық тең деуінің жалпы интегралы немесе жалпы шешімі

$$

$

$

$

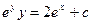
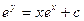
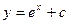
$$$248 п -ші ретті дифференциалдық тең деу деп...айтады.

$$тә уелсіз айнымалыны, ізделінді функцияны жә не п -ші ретті туындыны байланыстыратын тең деуді

$ізделінді функцияны жә не екінші ретті туындыны байланыстыратын тең деуді

$ізделінді функцияны жә не туындыны байланыстыратын тең деуді

$бір ө лшемді функцияларды байланыстыратын тең деуді

$$$249 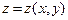функциясының 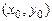нү ктесінде ү зіліссіз туындылары бар болса: ; ; 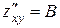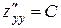, онда осы нү ктеде оның экстремум нү ктесі бар болуы да жоқ болуы да мү мкін, егер

$$

$

$

$

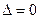
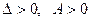
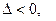
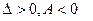
$$$250 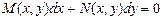дифференциалдық тең деуі толық дифференциалды дифференциалдық тең деу деп аталады, егер 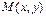пен 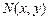функциялары ү зіліссіз 1-ші ретті туындылыры бар жә не келесі шарттарды қ анағ аттандыратын функциялар болса:

$$

$

$

$

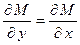
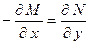
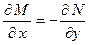
$$$251 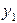мен 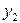- 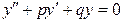дифференциалдық тең деуінің екі шешімі болсын 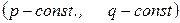. Келесі жағ дайлардың қ айсысында олар сызық ты тә уелсіз болады:

$$

$

$

$

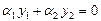
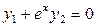
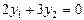
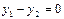
$$$252 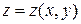функциясының 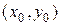нү ктесінде ү зіліссіз туындылары бар болса: ; ; 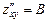, онда осы нү ктеде оның минимум нү ктесі болады, егер

$$

$

$

$

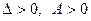
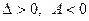
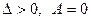
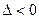
$$$253 Біртекті емес сызық ты дифференциалдық тең деу деп... айтады.

$$ізделінді функцияны, туындыны байланыстыратын жә не арнайы оң жағ ы берілген тең деуді

$ізделінді функцияны жә не туындыны байланыстыратын тең деуді

$ізделінді функцияны жә не екінші ретті туындыны байланыстыратын тең деуді

$тә уелсіз айнымалыны, ізделінді функцияны жә не туындыны байланыстыратын тең деуді

$$$254 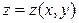функциясының 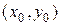функциясының: 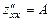, 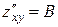; 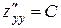, онда осы нү ктеде оның максимум нү ктесі болады, егер

$$

$

$

$

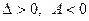
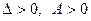
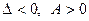
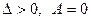
$$$255 Геометриялық ық тималдық тың формуласының тү рі:

$$

$

$

$

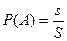
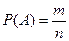
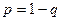
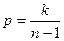
$$$256 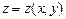функциясының 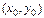функциясының: 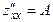, 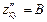; 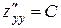, онда осы нү ктеде оның экстремум нү ктесі болмайды, егер

$$

$

$

$

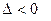
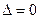
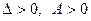
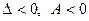
$$$257 Толық ық тималдық формуласын кө рсетің із

$$

$

$

$

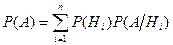
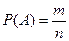
$$$258 Дискретті кездейсоқ шамалардың сандық сипаттамалары

$$ математикалық ү міт, дисперсия, орташа-квадраттық ауытқ у

$полигон мен гистограмма

$алмастыру, орналастыру, теру

$кездейсоқ шамалар

$$$259 А мен В оқ иғ алары ү йлесімсіз болса, онда...

$$

$

$

$

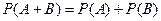
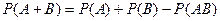
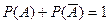
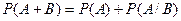
$$$260 Ү йлесімсі екі оқ иғ аның ең болмағ анда біреуінің пайда болу ық тималдығ ы:

$$

$

$

$

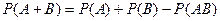
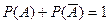
$$$261 Егер А мен В оқ иғ алары тә уелсіз болса, онда олардың бір уақ ытта пайда болу ық тималдығ ы...тең.

$$олардың ық тималдық тарының кө бейтіндісіне

$қ алғ ан оқ иғ алардың кө бейтіндісіне

$шартты ық тималдық тарының кө бейтіндісіне

$ық тималдық тарының қ осындысына

$$$262 Берілген қ атардың жинақ тылығ ының қ ажетті шартын кө рсетің із .

$$

$ ,

$ ,

$ ,

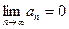
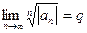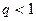
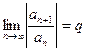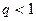
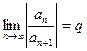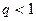
$$$263 Фурье қ атарының 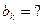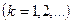коэффициенті қ ай формулмен табылады

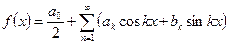, егер ,

$$

$

$

$

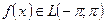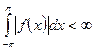
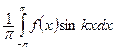
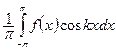
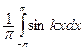
$$$264 Фурье қ атарының 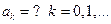коэффициенті қ ай формулмен табылады

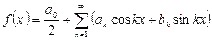, если ,

$$

$

$

$

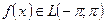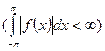
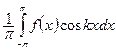
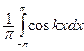
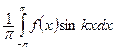
$$$265 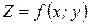функциясының 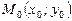нү ктесіндегі 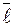векторының бағ ыты бойынша туындысы қ ай формуламен табылады

$$

$

$

$

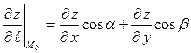
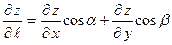
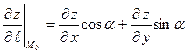
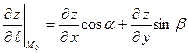
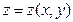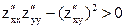$$$266 Егер функциясының кризис нү ктесінде келесі шартты қ анағ аттандыратын ү зіліссіз екінші ретті туындылары бар болса: и 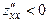, онда осы нү ктеде оның …нү ктесі болады.

$$максимум

$минимум

$экстремум

$экстремумы жоқ

$$$267 Егер 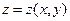функциясының 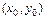кризис нү ктесінде келесі шартты қ анағ аттандыратын ү зіліссіз екінші ретті туындылары бар болса: 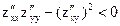и 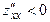, онда осы нү ктеде оның … нү ктесі болмайды.

$$экстремум

$максимум

$минимум

$экстремум бар

$$$268 Келесі формулалардың қ айсысы қ андайда бір екінші ретті коэффициенттері тұ рақ ты біртекті сызық ты дифференциалдық тең деудің жалпы шешімін анық тауы мү мкін:

$$

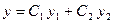
$2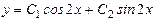

$

$

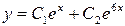
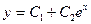
$$$269 Цехта 7 ер, 3 ә йел адам жұ мыс істейді. Табельдік номерлері бойынша кездейсоқ 5 адам таң далды. Осы адамдардың ішінде 3 ә йел адам болу ық тималдығ ын табың ыз.

$$1/12

$2/3

$3/10

$5/13

$$$270 Ә ртү рлі n элементтен кө лемі «m» орналастыру саны... тең.

$$

$

$

$

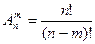
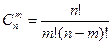
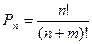
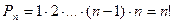
$$$271 Келесі ү лестірім функциясымен берілген Х кездейоқ шамасының математикалық ү мітін табың ыз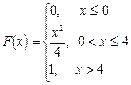

$$32/3

$1

$12/5

$0

$$$272 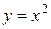, 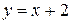қ исық тарымен шектелген фигураның ауданын табудың екі еселі интегралын жазың ыз

$$

$

$

$

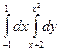
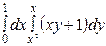
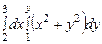
$$$273 Тең деуді шешің із: y¢ ¢ -6y¢ +5у=0, егер y=y(x)

$$

$

$

$

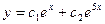
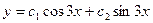
$$$274 Табу керек z_у¢, егер z=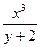

$$

$

$

$

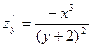
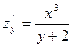
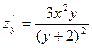
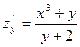
$$$275 М(1; 1) нү ктесіндегі z_у¢ табу керек, егер z=sin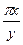

$$

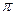
$cos1

$sin2

$-

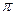
$$$276 М(0; 0; 1) нү ктесіндегі u_х¢ табу керек, егер u=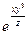

$$0

$

$

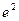
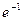
$3

$$$277 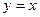, 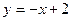жә не 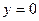қ исық тарымен шектелген ауданды табудың екі еселі интегралын жазың ыз

$$

$

$

$

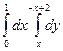
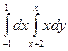
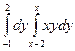
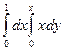
$$$278 Екі еселі интегралды есептең із: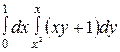

$$5/24

$1/8

$ 5/12

$3/5

$$$279 Екі еселі интегралды есептең із: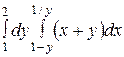

$$23/12

$-5/12

$7/3

$1/6

$$$280 Екі еселі интегралды есептең із: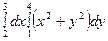

$$40

$56/7

$1/2

$17/24

$$$281 Екі мерген нысанағ а бір реттен оқ атады. Бірінші мергеннің оқ тигізу ық тималдығ ы– 0, 4, ал екіншінікі – 0, 5. Х кездейсоқ шамасының тү су санының ү лестірім заң ын анық таң ыз.

$$

$

$

$

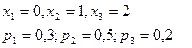
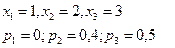
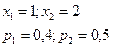
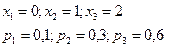
$$$282 n элементтердің алмастыру саны...

$$

$

$

$

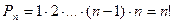
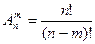
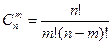
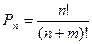
$$$283 Функцияның анық талу облысын табың ыз: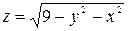

$$ радиусы 3 тең жарты сфера

$ радиусы 9 тең шең бер

$ радиусы 3 тең жарты шең бер

$ радиусы 9 тең сфера

$$$284 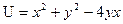функциясының 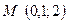нү ктесінен 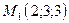нү ктесінің бағ ытындағ ы туындысын табың ыз

$$

$

$

$

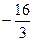
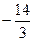
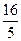
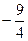
$$$285 Функцияның анық талу облысын табың ыз: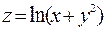

$$

$

$

$

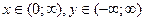
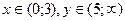
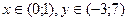
$$$286 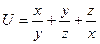функциясының нү ктесіндегі ө су жылдамдығ ының ең ү лкен мә нін табың ыз?

$$

$

$

$

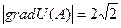
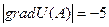
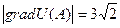
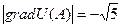
$$$287 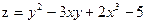функциясының 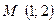нү ктесіндегі градиентін табың ыз

$$

$

$

$

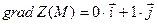
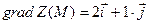
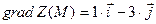
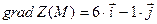
$$$288 Табу керек: М(ХУ), егер М(Х)=9 и М(У)=6

$$54

$3

$25

$0

$$$289 «n» элементтен «m» теру саны …тең.

$$

$

$

$

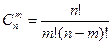
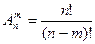
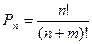
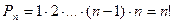
$$$290 Х кездейсоқ шамасының ү лестірім заң ы берілген:

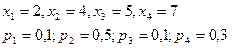Математикалық ү мітін табың ыз.

$$ 4, 8

$2, 7

$0, 5

$2, 1

$$$291 Х кездейсоқ шамасының ү лестірім заң ы берілген:

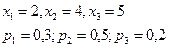М(х)-?

$$3, 6

$3

$2, 3

$4

$$$292 Қ атарды жинақ тылық қ а зерттең із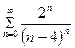

$$жинақ ты