Сумма модулей отклонений

плюсы:

- нечувствительность к выбросам.

минусы:

- сложность вычислительной процедуры;

- возможность больших отклонений между фактическими и проектными функциями;

- неоднозначность значений параметров и т.д.

Исходя из этих преимуществ и недостатков, обычно в качестве меры близости выбирают сумму квадратов и выбирают такую функцию y=f(x), у которой эта сумма квадратов достигает минимума.

Для того, чтобы лучше понять сущность метода наименьших квадратов, необходимо вначале вспомнить математические основы определения экстремума функции нескольких переменных.

В первую очередь, введем некоторые определения:

Определение 1. Функция Z = ƒ (x, y)имеет максимум в точке М₀ (х₀, у₀), если значение функции в этой точке больше значений ее в точках, достаточно близких к точке М₀ (х₀, у₀), т.е.

ƒ (х₀, у₀) > ƒ (х₀ + Δ х, у₀ + Δ у).

Это означает, что полное приращение функции Z = ƒ (х, у), вызванное переходом от точки (х₀, у₀) к соседней точке, будет величиной отрицательной:

Δ Z = ƒ (х₀ + Δ х, у₀ + Δ у) - ƒ (х₀, у₀) < 0. (2.1)

Определение 2. Функция Z = ƒ (x, y) имеет минимум в точке М₀ (х₀, у₀), если значение функции в этой точке меньше значений ее в точках, достаточно близких к точке М₀ (х₀, у₀), т.е.

ƒ (х₀, у₀) < ƒ (х₀ + Δ х, у₀ + Δ у).

Это означает, что полное приращение функции Z = ƒ (х, у), будет величиной положительной:

Δ Z = ƒ (х₀ + Δ х, у₀ + Δ у) - ƒ (х₀, у₀) > 0. (2.2)

Допустим, что функция Z = ƒ (х, у) имеет в точке М₀ (х₀, у₀) максимум или минимум (экстремум).Тогда для функции должно выполняться одно из неравенств (3.1) или (3.2) при любых, достаточно малых Δ х, Δ у.

Предположим, что Δ у = 0; тогда функция Z = ƒ (х, у) сделается функцией только одной переменной х. Эта функция по условию имеет экстремум.

Таким образом, условия обращения в нуль частных производных функции или несуществование хотя бы одной из них являются необходимыми условиями, но недостаточными условиями экстремума функции.

Имеем систему:

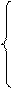
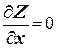
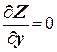. (2.4)

Условия (2.4) являются необходимыми для существования экстремума функции. Но может случиться, что эти условия в некоторых обстоятельствах невыполнимы.

Достаточные условия существования экстремума функции нескольких переменных имеют более сложный вид.

Пусть в точке М₀ (х₀, у₀) частные производные обращаются в нуль, т.е.

,.

Подсчитаем значения частных производных второго порядка функции

Z = ƒ (х, у) в этой точке и обозначим их соответственно буквами: А, В, С:

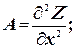
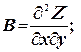
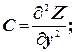
тогда:

1. Если АС - В² > 0, то функция Z = ƒ (х, у) имеет в точке М₀ (х₀, у₀) экстремум, а именно:

при А < 0 максимум,

при А > 0 минимум.

2. Если АС - В² < 0, то функция Z = ƒ (х, у) не имеет в точке М₀ (х₀, у₀) экстремума.

3. Если АС - В² = 0, то вопрос о существовании экстремума функции в точке М₀ (х₀, у₀) остается открытым и требуются дополнительные исследования.

Метод наименьших квадратов является одним из важных применений теории экстремума функции нескольких переменных.

Предположим, что в результате некоторого опыта или наблюдения установлена зависимость между переменными величинами х и у, выражаемая в виде таблицы:

Пусть требуется перейти от табличного метода задания функции к аналитическому (т.е. выраженному в виде формулы), причем, если это нельзя сделать точно, постараемся получить аналитическую связь приближенно.

Теперь обратимся к графическому изображению данной системы. Рассматривая значения х и у как координаты точек в прямоугольной системе координат, наносим эти точки на график. Пусть, например, построенные точки расположены достаточно близко к некоторой прямой. Поэтому можно приблизительно считать, что между х и у существует линейная зависимость, выражаемая формулой,

у = ах + b.

Поставим задачу аналитического определения неизвестных коэффициентов а и b.

В основе аналитического метода определения а и b лежит метод наименьших квадратов. Точки, полученные на основании опытных данных, вообще говоря, не лежат на искомой прямой. Если бы некоторая точка (х_i, у_i) лежала на прямой, то ее координаты удовлетворяли бы уравнению прямой, т.е. имело бы место равенство:

у_i = ax_i + b или ax_i + b - y_i = 0

Однако в общем случае подстановка координат точки в уравнение прямой дала бы:

ax_i + b - y_i = ε _i,

где ε _i ─ какая то малая величина.