й учебный вопрос. Интерпретация и ошибки коэффициентов парной регрессии.

Очень важно иметь в виду, что уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.

Коэффициент при х, называемый коэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.

В нашем примере коэффициент регрессии получился равным 24, 5. Это означает, что с увеличением посева, приходящегося на душу, на одну десятину, сбор хлеба на душу населения в среднем увеличивается на 24, 5 пуда.

Средняя и предельная ошибки коэффициента регрессии. Поскольку уравнения регрессии рассчитываются, как правило, для выборочных данных, обязательно встают вопросы точности и надежности полученных результатов. Вычисленный коэффициент регрессии, будучи выборочным, с некоторой точностью оценивает соответствующий коэффициент регрессии генеральной совокупности. Представление об этой точности дает средняя ошибка коэффициента регрессии (μ _a1), которая рассчитывается по формуле:

μ _a1 = σ _y(x) / (σ _x√ n) (2.16)

где

σ _y(x) = √ Σ (у_i - ŷ _i)²/(n-m-1) (2.17)

у_i, — i-e значение результативного признака; ŷ _i — i-e выравненное значение, полученное на основе уравнения (2.15); x_i —i-e значение факторного признака; σ _x—среднее квадратическое отклонение х; n — число значений х или, что то же самое, значений у; m —число факторных признаков (независимых переменных).

В формуле (2.17), в частности, формализовано очевидное положение: чем больше фактические значения отклоняются от выравненных, тем большую ошибку следует ожидать; чем меньше число наблюдений, на основе которых строится уравнение, тем больше будет ошибка.

Средняя ошибка коэффициента регрессии является основой для расчета предельной ошибки. Предельная ошибка показывает, в каких пределах находится истинное значение коэффициента регрессии при заданной надежности результатов. Предельная ошибка коэффициента регрессии вычисляется аналогично предельной ошибке средней величины выборки, т. е. как t μ _a1 где t —величина, числовое значение которой определяется по таблице распределения Стьюдента.

Найдем среднюю и предельную ошибки коэффициента регрессии, полученного в рассмотренном примере. Для расчета μ _a1 прежде всего подсчитаем выравненные по регрессии (или расчетные) значения ŷ _i. Для этого в уравнение регрессии, полученное в примере, подставим конкретные значения x_i:

ŷ _i = 17, 8 +24, 5*0, 91 = 41, 22 и т. д.

Затем вычислим отклонения фактических значений у_i, от выравненных и их квадраты.

Далее, подсчитав средний по губерниям посев на душу населения ( =0, 98), найдем отклонения фактических значений x_i от этой средней, квадраты отклонений, дисперсию и среднее квадратическое отклонение 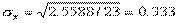, получим все необходимые составляющие формул (2.16) и (2.17):

Таким образом, средняя ошибка коэффициента регрессии a ₁ равна 2, 89, что составляет 12% от вычисленного значения коэффициента a ₁.

Заключение. Таким образом, на данной лекции мы рассмотрели математические основы и теоретические предпосылки метода наименьших квадратов (МНК) и пример его использования для построения уравнения парной линейной регрессии. Рассмотрели также понятия «несмещенные», «эффективные» и «состоятельные» оценки параметров регрессии и способы проверки предпосылок МНК. Затем, на конкретном примере было рассмотрено понятие средней и предельной ошибки параметра уравнения регрессии.