
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критические (пограничные значения) статистики Дарбина-Уотсона
|
|
| n | K=1; m=2 | K = 2; m=3 | K=3; m=4 | |||
| d0 | d1 | d0 | d1 | d0 | d1 | |
| 0, 88 | 1, 32 | 0, 70 | 1, 64 | 0, 53 | 2, 02 | |
| 1, 08 | 1, 36 | 0, 95 | 1, 54 | 0, 82 | 1, 75 | |
| 1, 2 | 1, 41 | 1, 1 | 1, 54 | 1, 68 | ||
| 1, 35 | 1, 49 | 1, 28 | 1, 57 | 1, 21 | 1, 65 |
Пограничные значения, в которых должна находиться величина d, приведенные в табл. 6.1., зависят от числа наблюдений n (длины ряда данных) и числа переменных K или параметров m уравнения регрессии).
Если d< d0 , то гипотеза об отсутствии автокорреляции отвергается
(с вероятностью 0, 95).
Если d> d1, то гипотеза об отсутствии автокорреляции принимается с вероятностью 0, 95.
Если d0 ≤ d ≤ d1 , то нет достаточных оснований для того, чтобы принять или отвергнуть гипотезу об отсутствии автокорреляции. Рекомендуется увеличить число переменных n.
Такая проверка осуществляется, если 0 ≤ d < 2. Если 2 < d ≤ 4, то имеется так называемая отрицательная автокорреляция и с критическими значениями d0 и d1 сравнивается величина 4-d.
Проверка соответствия распределения остаточной компоненты нормальному закону производится с использованием статистических критериев, например критерия Пирсона, критерия Колмогорова и др. которые будут более подробно рассмотрены на следующей лекции. Однако на практике применение критериев согласия затруднено из-за небольшого объема статистических данных (п< 50), поэтому оценка соответствия нормальному закону может быть осуществлена приближенно с использованием показателей асимметрии и эксцесса.
При нормальном распределении показатели асимметрии (А) и эксцесса (Э) рассчитываются по формулам:
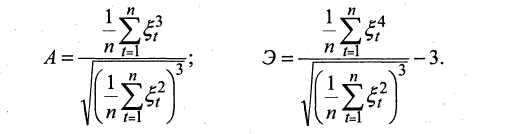
Если одновременно выполняются неравенства:
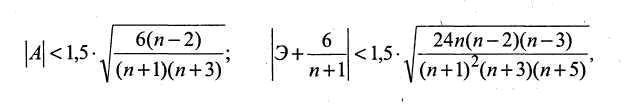
то гипотеза о нормальном законе распределения принимается.
Если выполняются хотя бы одно из неравенств:
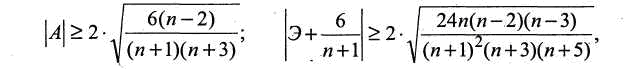
то гипотеза о нормальном законе распределения отвергается.
В других случаях требуется дополнительная проверка с помощью более мощных критериев.
Заключение.
На лекции были рассмотрены способы линеаризации нелинейных уравнений регрессии и построение систем нормальных уравнений для расчета параметров различных типов уравнений. Особо было отмечено, что при линеаризации уравнений, нелинейных по параметрам, могут нарушиться предпосылки МНК, поэтому их необходимо проверять после построения таких уравнений. Были рассмотрены способы проверки предпосылок МНК о поведении величин остатков уравнений регрессии. На следующей лекции мы рассмотрим статистические критерии, которые используются для проверки нормального закона распределения случайной величины.