
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Й учебный вопрос. Способы проверки гипотезы о наличии тренда.
|
|
Основные подходы к решению этой задачи основаны на статистической проверке гипотез. Критерии выявления компонент ряда основаны на проверке гипотезы о случайности ряда.
Рассмотрим наиболее часто используемые на практике критерии
проверки " наличия-отсутствия" тренда: критерий восходящих и нисходящих серий; критерий серий, основанный на медиане выборки и метод Фостера-Стюарта.
Критерий " восходящих и нисходящих" серий реализуется в виде
следующей последовательности шагов:
1) Для временного ряда у1, y2,..., yt..., yn определяется последовательность, исходя из следующих условий:

| +, если yt+1 – yt> 0, для t = 1÷ n-1 | |||
| δ i | = | |||
| –, если yt+1 – yt< 0, для t = 1÷ n-1 |
Индекс i может изменяться от 1 до (n-1). В случае, когда последующее
наблюдение окажется равным предыдущему, учитывается только одно
наблюдение.
Таким образом, элементы этой последовательности принимают значение " +", если последующее значение уровня ряда yt+1 больше предыдущего yt, и " -" - в противном случае.
2) Подсчитывается v(n) - число серий в совокупности δ i(i = 1÷ n-1), где под серией понимается последовательность подряд идущих плюсов или минусов. Один плюс или один минус тоже будет считаться серией.
3) Определяется τ max (n)- протяженность самой длинной серии.
4) Проверка гипотезы основывается на том, что при условии случайности ряда (при отсутствии систематической составляющей) протяженность самой длинной серии не должна быть слишком большой, а общее число серий - слишком маленьким. Поэтому, если нарушается хотя бы одно из следующих неравенств, то гипотеза об отсутствии тренда (гипотеза о случайности) отвергается для 5% уровня значимости (с доверительной вероятностью 0, 95).
 (1.5),
(1.5),
где: n – длина временного ряда;
v(n) – число серий;
τ max(n) – число подряд идущих плюсов или минусов в самой длинной серии.
Величина τ 0 (n) – табличное значение, зависящее от n-длины исходного ряда.
| Длина ряда | n ≤ 26 | 26 < n ≤ 153 | 153 < n ≤ 170 |
| Значение τ 0 (n) |
Квадратные скобки в правой части неравенства (1.5.) означают целую часть числа. Напомним, что целая часть числа А - [А] - это целое число, ближайшее к А и не превосходящее его.
Рассмотрим теперь критерий серий, основанный на медиане выборки.
Этот критерий гипотезу о случайности временного ряда проверяет
следующим образом:
1) из исходного ряда yt длиной n образуется ранжированный (вариа-
ционный) ряд y't: у'1, у'2..., у'n, где у'1, наименьшее значение ряда yt.
2) Определяется медиана этого вариационного ряда Ме. В случае нечетного значения n (n = 2m+1) Ме = у'm+1, в противном случае
Ме=(у'm + у'm+1): 2.
3) Образуется последовательность δ i из плюсов и минусов по сле-
дующему правилу:

| +, если yt > Me, t = 1, 2,..., n | |||
| δ i | = | |||
| –, если yt< Me, t = 1, 2,..., n |
Если значение yt равно медиане, то это значение опускается.
4) Подсчитывается протяженность самой длинной серии τ max (n) и
общее число серий v(n) аналогично тому, как это делалось в критерии
" восходящих и нисходящих" серий.
5) Для того, чтобы не была отвергнута гипотеза о случайности ис-
ходного ряда (об отсутствии систематической составляющей) должны вы-
полняться следующие неравенства (для 5% уровня значимости);
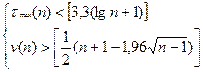
 (1.7.)
(1.7.)
Если хотя бы одно из неравенств нарушается, то гипотеза об отсутствии тренда отвергается.
Другой способ проверки гипотезы о наличии тенденции процесса
основывается на методе Фостера-Стюарта. Этот метод может быть реали-
зован в виде следующей последовательности шагов:
1) Каждый уровень ряда сравнивается со всеми предшествующими,
при этом определяются значения вспомогательных характеристик mt и lt:

| mt =1, если yt > yt-1, yt-2,..., y1 | |||
| mt | = | |||
| mt =0, в противном случае сссслслучаеслучае |

| lt =1, если yt < yt-1, yt-2,..., y1 | |||
| lt | = | |||
| lt =0, в противном случае |
Таким образом, mt = 1, если yt больше всех предшествующих уровней, а lt =1, если yt меньше всех предшествующих уровней.
2) Вычисляется dt = mt-lt для всех t = 2÷ n
Очевидно, что величина dt может принимать значения 0; 1; - 1.
3) Находится характеристика 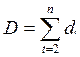
4) С помощью критерия Стьюдента проверяется гипотеза о том, что
можно считать случайной разность D-0 (т.е. ряд можно считать случайным, не содержащим тренд).
Для этого определяется:
tнабл = 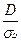 ,
,
где σ D -средняя квадратическая ошибка величины D:

Значения σ D находятся на основе специальной таблицы (табл.8.1).
Расчетное значение tнабл сравнивается с критическим значением tкр, взятым из таблицы t-распределения Стьюдента для заданного уровня значимости α и числа степеней свободы k = n - 1. Если tнабл > tкр, то гипотеза об отсутствии тренда отвергается.
Таблица 8.1.