
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гранные поверхности и многогранники
|
|
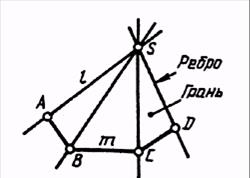
Гранные поверхности образуются перемещением прямолинейной образующей по ломанной направляющей. При этом, если одна точка образующей (S) неподвижна, создается пирамидальная поверхность (рис. 5.2.1.а). Если образующая параллельна заданному направлению, то создается призматическая поверхность (рис.5.2.1.б).

а б
Рисунок 5.2.1
Замкнутые гранные поверхности называются многогранниками. Элементами многогранников являются:
· вершина – точка S образующей (у призмы она находится в бесконечности);
· грань - часть плоскости, ограниченная направляющей и образующими;
· ребро – линия пересечения соседних граней;
· основание – часть плоскости, ограниченная направляющей.
Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани. Из всего многообразия выпуклых многогранников наибольший практический интерес представляют: пирамиды, призмы, призматоиды.
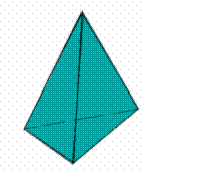
Пирамида это многогранник, в основании которого лежит произвольный многоугольник, а боковые грани — треугольники с общей вершиной S (5.2.2.а).
а б
Рисунок 5.2.2
Призма — многогранник, у которого основания это два одинаковых и взаимно параллельных многоугольника, а боковые грани — параллелограммы (рис. 5.2.2.б).
На комплексном чертеже многогранники задают проекциями их вершин и ребер с учетом видимости. Видимость ребер определяют с помощью конкурирующих точек.
Любую точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку.
На рис. 5.2.3. приведен пример построения на комплексном чертёже пирамиды ABCD точки М, принадлежащей грани ABC. Если по условию задачи известна фронтальная проекция точки М2, то через нее на плоскости A2B2C2 проводится прямая С252, а затем с помощью линий связи находится горизонтальная проекция С151. Горизонтальная проекция точки М находится на С151 и определяется с помощью линии связи, проведенной из М2.
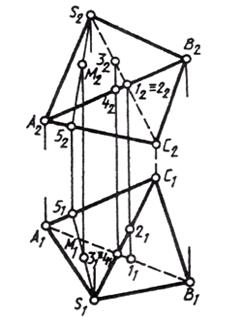
Рисунок 5.2.3
На рис. 5.2.4 дан комплексный чертеж прямой четырехугольной призмы с горизонтально проецирующей поверхностью.
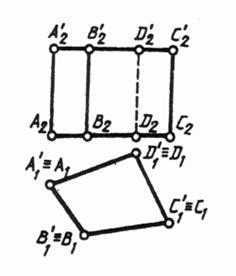
Рисунок 5.2.4
Если ребра призмы перпендикулярны плоскостиоснования, такую призму называют прямой. Если у призмы ребра перпендикулярны какой-либо плоскости проекций, то боковую поверхность ее называют проецирующей.
ЛЕКЦИЯ №5: Поверхности (продолжение).