Исследование свойств выборочного среднего

ЛАБОРАТОРНАЯ РАБОТА

Цель работы:

Исследование статистическими методами сходимости по вероятности выборочного среднего.

Основные соотношения:

Выборочное среднее 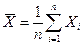с точки зрения математической статистики есть среднее арифметическое независимых одинаково распределенных случайных величин 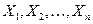. Следовательно, если для генеральной существуют конечные математическое ожидание и дисперсия, то для выборочного среднего справедлив закон больших чисел Чебышева.

Теорема (Закон больших чисел в форме Чебышева). Если 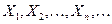- последовательность независимых и одинаково распределенных случайных величин, имеющих конечные математическое ожидание 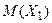и дисперсию 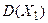, то среднее арифметическое этих величин сходится по вероятности к их математическому ожиданию:

,

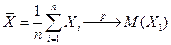или, для любого 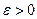: 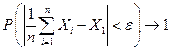при .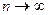

Статистически данное утверждение можно проверить следующим образом. Генерируем последовательности случайных величин разной длины, вычисляем среднее значение для каждой последовательности и сравниваем с математическим ожиданием величин (поскольку мы сами генерируем случайные последовательности, то математическое ожидание генеральной совокупности нам известно). Если условия теоремы Чебышева выполняются, то с ростом 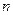величина отклонения выборочного среднего 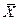от математического ожидания величин 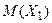должна в среднем уменьшаться. Чтобы учесть случайный характер отклонений, следует для каждой длины последовательности генерировать несколько выборок (последовательностей) значений и сравнивать либо средние значения отклонений для выборок различного объема, либо величины разброса значений 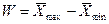. Кроме того, если наблюдается сходимость по вероятности, то всегда можно для заданной величины отклонения 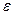и вероятности 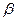определить необходимый объем выборки N, так, чтобы 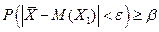. Это можно сделать, например, используя центральную предельную теорему (ЦПТ). Согласно ЦПТ, если 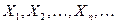- независимые и одинаково распределенные случайных величины, имеющих конечные математическое ожидание 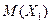и дисперсию 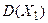, то их среднее (при 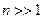) имеет приближенно нормальное распределение с математическим ожиданием 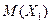и дисперсией . Тогда:

,

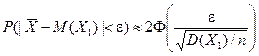где 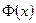- функция Лапласа. Разрешив уравнение:

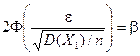
относительно n, получим необходимый объем выборки N. Определив N, можно убедиться, что величина отклонения не превышает 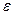(с вероятностью 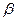), сгенерировав несколько последовательностей длиной N и подсчитав для каждой из них величину отклонения выборочного среднего от математического ожидания.

Если для генеральной совокупности не существует конечного математического ожидания, то сходимость выборочного среднего в этом случае не должна наблюдаться (то есть разброс значений выборочных средних в этом случае с ростом объема выборок не должен уменьшаться).