Генерация случайных чисел по законам, отсутствующим в пакете EXCEL.

Для генерации случайных чисел распределенных по законам, которые отсутствуют в генераторе случайных чисел пакета EXCEL, можно использовать следующие приемы.

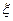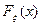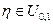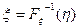1. Воспользуемся следующей теоремой из курса “Теория вероятностей”: Если случайная величина имеет непрерывную и строго монотонную функцию распределения , а величина , то , где 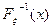- функция обратная к 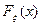. Итак, если 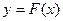- функция распределения непрерывной случайной величины, для которой можно найти обратную 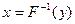, то генерируя случайную величину 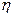, равномерно распределенную на 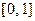, получим величину 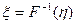с требуемой функцией распределения . Данный прием можно использовать для генерации случайных величин, распределенных по показательному закону, по закону Коши и др.

2. Если случайная величина есть композиция других случайных величин, то генерируем эти величины и строим из них искомую величину. Данный прием можно использовать, например, для получения случайных величин распределенных по законам 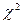, Стьюдента и др. Так, случайной величиной, имеющей распределение " хи-квадрат" с 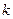степенями свободы называют величину равную сумме квадратов 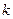независимых стандартных нормальных случайных величин, т.е. 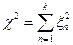, 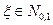. Случайной величиной 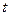, имеющей распределение Стьюдента с 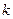степенями свободы называют величину равную 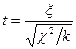, где 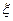- случайная величина распределенная по закону 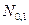, а 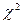- независимая от нее случайная величина распределенная по закону хи-квадрат с 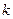степенями свободы.

3. Используем “физический” смысл случайной величины. Например, случайная величина, распределенная по геометрическому закону, есть номер первого успешного испытания в бесконечной серии испытаний по схеме Бернулли. Тогда, можно сгенерировать последовательность случайных величин, распределенных по закону Бернулли, и определить порядковый номер всех единиц в этой последовательности, сбрасывая счетчик после появления каждой единицы в ноль. Последовательность номеров, очевидно, будет иметь геометрическое распределение. Приблизительно необходимую длину исходной последовательности можно оценить следующим образом: если 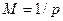- среднее число попыток до наступления успеха, то потребуется в среднем 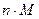чисел, распределенных по закону Бернулли.