Обчислювальна математика

Самостійна робота № 16

4.1.3. Наближене розв’язування рівнянь. Метод половинного ділення.

Навчальна мета: знати теорію розв’язання рівнянь методом половинного ділення, відновити у пам’яті правила побудови рівнянь гармонічних коливань, логарифмічної показникової функції.

Розвивальна мета: розвивати швидкі та точні обчислювальні навички, увагу, пам’ять, спостережливість, шляхом розв’язування завдань.

Виховна мета: виховувати уважність та акуратність.

Література

1. Данко П.Е. Высшая математика в упражнениях и задачах [Текст]: учебное пособие для студентов втузов. В 2-х ч. Ч 1 / П.Е. Данко, А.Г. Потапов, Т.Я. Кожевникова. – М.: Высш. шк.., 1986. – 304 с.: илл.

2. Данко П.Е. Высшая математика в упражнениях и задачах [Текст]: учебное пособие для студентов втузов. В 2-х ч. Ч 2 / П.Е. Данко, А.Г. Потапов, Т.Я. Кожевникова. – М.: Высш. шк., 1986. – 415 с.: илл.

3. Дидактичні матеріали з математики [Текст]: навч. посібник / О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов [та ін.]. – К.: Вища школа, 2001. – 271 с.: іл.

4. Математика [Текст]: підручник / О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов [та ін.]. – К.: Вища школа, 2001. – 447 с.: іл.

5. Письменный Д.Т. Конспект лекций по высшей математике: полный курс [Текст]: курс лекций / Дмитрий Трофимович Письменный. – М.: Айрис-пресс, 2006. – 608 с.: илл.

6. Сборник задач по высшей математике. 1 курс [Текст]: сборник задач / К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин [и др.]. – М.: Айрис-пресс, 2008. – 576 с.: илл.

Побудова графіків гармонічного коливання.

Приклад 1. Дана функція 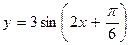. Описати, як виглядає її графік.

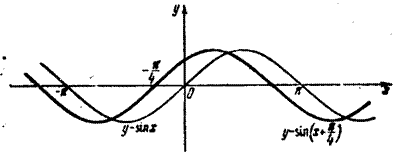
Це деформована синусоїда. Дану функцію представимо таким чином: .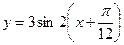

Так як k = 3 > 0, то синусоїда розтягнута вздовж осі ординат; так як a = 2 > 0, то синусоїда стиснута вздовж осі абсцис; так як φ ₀ = 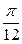> 0, то синусоїда зміщена вліво вздовж осі абсцис на відрізок довжини .

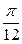В цілому, для побудови графіка функції 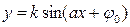, a ≠ 0, її представляють таким чином: 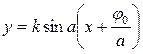. Тоді легко побачити, що графік цієї функції утворюється з графіка функції 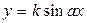зміщенням вздовж осі абсцис на відрізок довжини 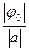вліво, якщо 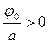, та вправо, якщо .

Побудова графіка функції.

Приклад 2. Дана функція 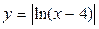. Описати, як побудувати її графік.

Так як a= -4 < 0, то графік зміщений вправо вздовж осі абсцис на відрізок довжини 4.

Будуємо графік 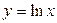; зміщуємо його по осі Ох на 4 одиниці праворуч; симетрично відображаємо частину графіка, яка відповідає від’ємному значенню функції y, відносно осі Ох.