Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поняття визначеного інтеграла
|
|
Означення: Якщо існує скінченна границя інтегральних сум Sn при lіà 0 і не залежить ні від способу розбиття [a; b] на частини Dхі, ні від вибору точок xі, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a; b] і позначається:
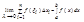
За означенням, визначений інтеграл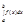 
– число, яке залежить від типу ф-ії f(x) та проміжку [a; b]; він не залежить від того, якою буквою позначена змінна інтегрування.
Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною.
54.Обчислення визначених інтегралів.Формула Ньютона-Лейбніца.
Визначенні інтеграли можна обчислити за:
- формулою ньютона-лейбніца
- методом підстановки або заміни
- методом інтегрування частинами
Для обчислення визначеного інтеграла при умові існування первісної користуються формулою Ньютона-Лейбніца:
З цієї формули видно порядок обчислення визначеного інтегралу:
1. знайти невизначений інтеграл від даної функції;
2. в отриману первісну підставити на місце аргументу спочатку верхню, а потім нижню межу інтеграла;
3. знайти приріст первісної, тобто обчислити інтеграл
