Визначення рівнодійної системи збіжних сил методом проекції.Аналітична умова рівноваги.

Систему сил називають збіжною, якщо лінії дії сил перетинаються в одній точці.

Згідно з аксіомою про паралелограм сил рівнодійна цієї системи сил дорівнює геометричній сумі складових сил:

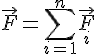
Щоб дати аналітичне визначення ковзного вектора рівнодійної, треба знайти її момент відносно довільної точки O:

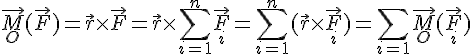
Згідно з моментом рівнодійної відносно довільного центра дорівнює геометричній (векторній) сумі моментів складових сил відносно того самого центра.

Наведене твердження є змістом теореми Варіньйона щодо збіжної системи сил.

Умовою рівноваги збіжної системи сил є рівність нулеві їх рівнодійної:

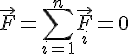
Умова рівноваги є як необхідною, так і достатньою, бо з неї випливає рівність нулеві обох компонент ковзного вектора .

Умову називають ще механічною, або фізичною, умовою рівноваги збіжної системи сил.

Очевидно, що багатокутник сил за замкнений. У цьому полягає геометрична (графічна) умова рівноваги.

На підставі проекції рівнодійної сили на осі прямокутної декартової системи координат дорівнюють алгебраїчним сумам проекцій складових сил на осі координат

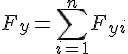
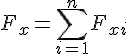
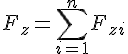
Отже, згідно з механічною умовою рівноваги на підставі дістаємо аналітичні умови рівноваги збіжної системи сил:

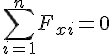
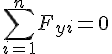
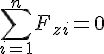
Рівності називають аналітичними рівняннями рівноваги.

У разі потреби з них можна знайти не більш як три алгебраїчних невідомих.

Якщо кількість невідомих перевищує кількість рівнянь рівноваги, задачу називають статично невизначеною.