
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Процедура оценивания погрешности
|
|
Вычисление значения измеряемой величины
Пусть модель объекта (измеряемой величины)
Х = ƒ (X 1, X 2, …, Xm) – Δ мет;
при измерениях получены результаты наблюдений Х ij,
где i = 1, …, m – количество прямо измеряемых входных величин;
j = 1, …, n – число наблюдений каждой входной величины.
Порядок нахождения 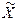 :
:
1) исключение известных систематических погрешностей путем введения поправок Δ c ij :
Х΄ ij = Хij – Δ c ij ;
2) оценка равноточности измерений (исключение грубых погрешностей)
– по критерию Смирнова или критерию Райта;
3) 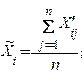 вычисление среднего арифметического каждой входной величины:
вычисление среднего арифметического каждой входной величины:
4) вычисление значения измеряемой величины:
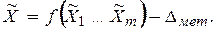
При связанных входных величинах сначала вычисляют ряд
Х'j = ƒ (X' 1 j, …, X'mj) – Δ мет, а затем 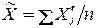 .
.
Процедура оценивания погрешности
На практике невозможно получить бесконечное множество показаний при сохранении неизменности условий, при которых выполняются измерения. Поэтому в процессе обработки результатов измерений могут быть получены только оценки этих числовых характеристик. Оценки, получаемые по статистическим данным, являются случайными величинами, и их значения зависят от объема экспериментальных данных. Оценки должны быть состоятельными, несмещенными и эффективными.
- состоятельная – если при увеличении числа наблюдений она стремиться к истинному значению оцениваемой величины;
- несмещенная – если ее математическое ожидание равно истинному значению оцениваемой величины;
- эффективная – если можно найти несколько несмещенных оценок, лучшая из них считается та, которая имеет наименьшую дисперсию.
1) вычисление оценок СКО
– входных величин:
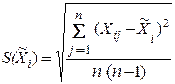 ;
;
– результата измерения:
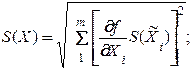
2) определение доверительных границ случайной составляющей погрешности:
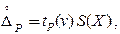
tP(v) – квантиль распределения Стьюдента для заданной Рд при числе степеней свободы v = n – 1.
3) вычисление границ и СКО неисключенной систематической составляющей погрешности:
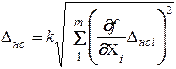 ,
, 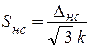 ,
,
k = 1, 1 при Рд = 0, 95;
Δ нсi определяется по имеющейся информации;
4) вычисление СКО суммарной погрешности:
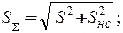
5) оценка погрешности измерения
– если Δ нс / S(Х) < 0, 8, то 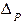 =
= 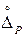 ; (систематической погрешностью пренебрегают и определяют доверительные границы погрешности результата как доверительные границы случайной погрешности)
; (систематической погрешностью пренебрегают и определяют доверительные границы погрешности результата как доверительные границы случайной погрешности)
– если Δ нс / S(Х) > 8, то 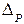 = Δ нс; (то случайной составляющей погрешности пренебрегают)
= Δ нс; (то случайной составляющей погрешности пренебрегают)
– если 0, 8 ≤ Δ нс / S(Х) ≤ 8, то 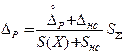 ; (доверительные границы погрешности результата определяют по композиции двух законов распределения).
; (доверительные границы погрешности результата определяют по композиции двух законов распределения).
6) интерпретация полученных результатов:
· интервал (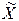 – Δ Р,
– Δ Р, 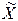 + Δ Р) с вероятностью Рд содержит истинное значение измеряемой величины.
+ Δ Р) с вероятностью Рд содержит истинное значение измеряемой величины.