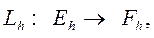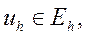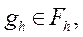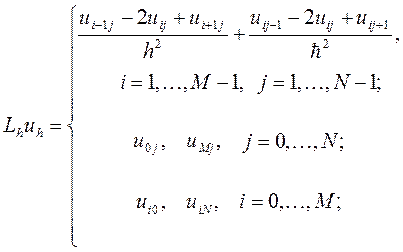Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Разностная схема. Разностная схема для эллиптического уравнения
|
|
Разностная схема для эллиптического уравнения
Постановка задачи
Рассмотрим задачу Дирихле для уравнения
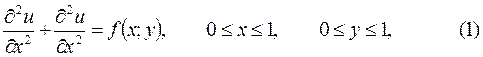
 y
y
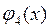

 1
1
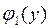 D
D 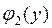
 0
0 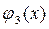 1 x
1 x
с краевыми условиями

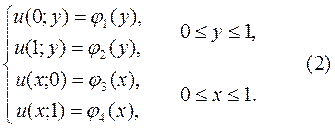
Будем считать, что правая часть дифференциального уравнения 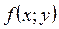 и функции
и функции 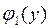 ,
, 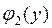 ,
, 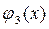 ,
, 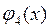 удовлетворяет условиям, обеспечивающим существование и единственность гладкого решения
удовлетворяет условиям, обеспечивающим существование и единственность гладкого решения 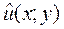 задачи (1) - (2).
задачи (1) - (2).
Разностная схема
Построим разностную схему - разностный аналог дифференциальной задачи (1) - (2).
Выполним следующие шаги:
1) Область непрерывного изменения аргументов 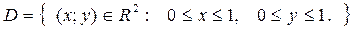 заменим дискретным множеством точек – сеткой
заменим дискретным множеством точек – сеткой 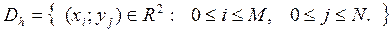 ,
, 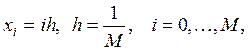
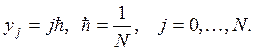 Точки
Точки 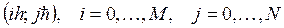 называются узлами сетки
называются узлами сетки 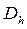 ,
, 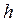 и
и 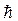
 называются шагами сетки по оси
называются шагами сетки по оси 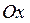 и
и 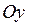 , соответственно. Узел
, соответственно. Узел  сетки
сетки 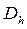 будем обозначать
будем обозначать 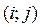 . Обозначим множество внутренних узлов сетки через
. Обозначим множество внутренних узлов сетки через 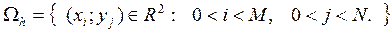 и через
и через 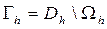 - множество граничных узлов.
- множество граничных узлов.
Сетку 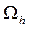 можно представить в виде
можно представить в виде
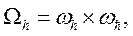
где 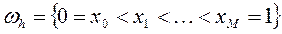 ,
, 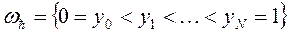 .
.
Замечание. При реализации метода сеток шагиобычно выбирают согласованно. Поэтому сетка и обозначена через 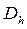 .
.
2) Все функции в исходной дифференциальной задаче (1) – (2) заменим сеточными функциями - функциями, определенными в узлах сетки 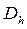 . Сеточную функцию обозначим через
. Сеточную функцию обозначим через 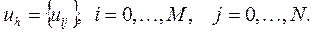 Проекцию функции
Проекцию функции 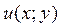 на сетку
на сетку 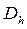 обозначим через
обозначим через 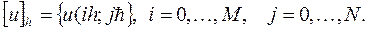
3) Производные в исходной дифференциальной задаче (1) – (2) заменим разностными отношениями – сходящимися формулами численного дифференцирования:
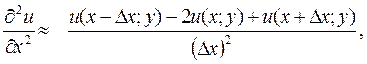

В результате получим систему линейных алгебраических уравнений:
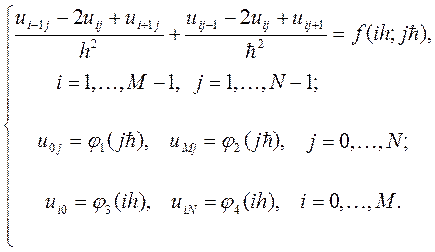 (3)
(3)
Система (3) называется разностной схемой - разностным (дискретным) аналогом дифференциальной задачи (1) – (2).
Для построения разностной схемы (3) используется пять точек – пяти-точечный шаблон:
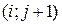
 |


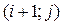
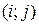
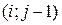
Введем пространства сеточных функций 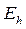 и
и 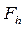 .
.
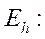
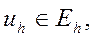
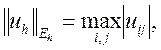
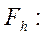
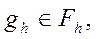
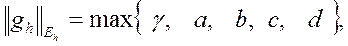
где 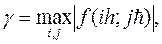
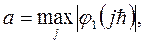
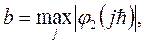
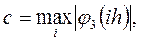
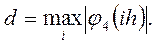
Теперь разностную схему (3) можно записать в виде операторного уравнения

где