Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аппроксимация и устойчивость разностной схемы
|
|
Введем пространства 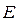 - функций
- функций 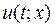 непрерывных на D и имеющих, непрерывные частные производные
непрерывных на D и имеющих, непрерывные частные производные 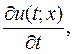
 и пространство
и пространство 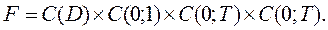 :
:
Теперь дифференциальную задачу (1)-(2) можно записать в виде операторного уравнения:
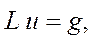
где 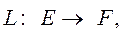
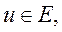
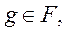
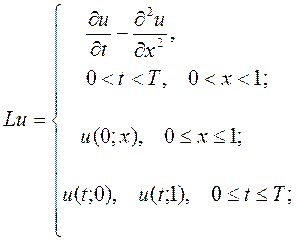
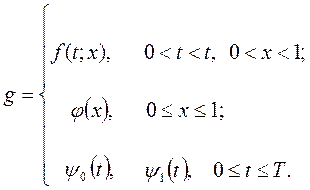
Введем пространства сеточных функций 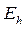 и
и 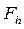 .
.

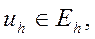
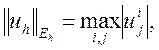
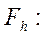
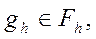
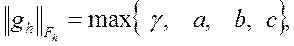
где 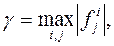
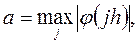
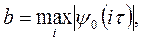

Теперь разностную схему (3) можно записать в виде операторного уравнения
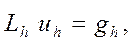
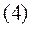
где 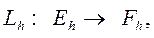
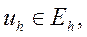
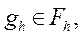
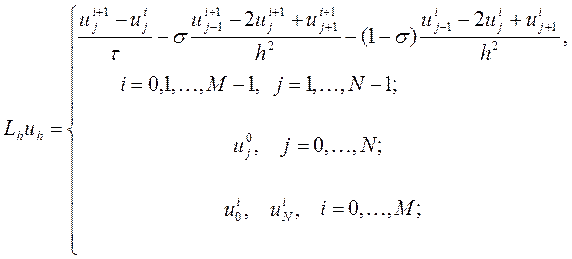
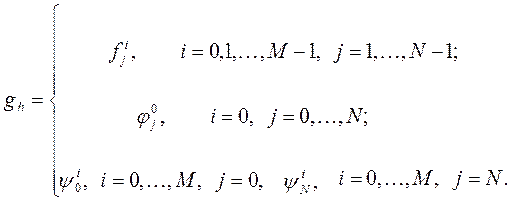
Замечание. Операторы 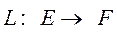 и
и 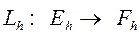 линейные и ограниченные.
линейные и ограниченные.
По определению разностная схема (4) аппроксимирует исходную дифференциальную задачу (1) - (2) на ее решении 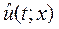 если
если
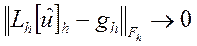 при
при 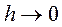
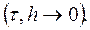 .
.
При этом, если существует константа 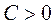 не зависящая от
не зависящая от 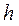 , и
, и
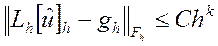 при
при 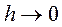
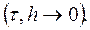 ,
,
то будем говорить, что разностная схема (4) аппроксимирует задачу (1)-(2) с порядком 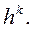
Разность 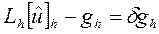 называется невязкой.
называется невязкой.
Пусть  . Введем в рассмотрение промежуточный слой по
. Введем в рассмотрение промежуточный слой по 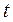 :
:
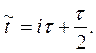
Тогда
а) 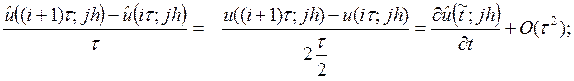
б) 
Следовательно,

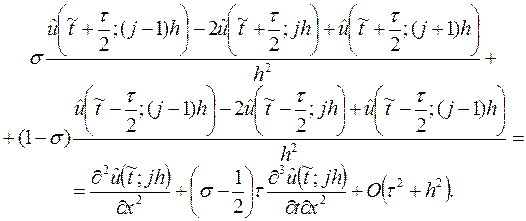
Так как для краевых условий на промежуточном слое
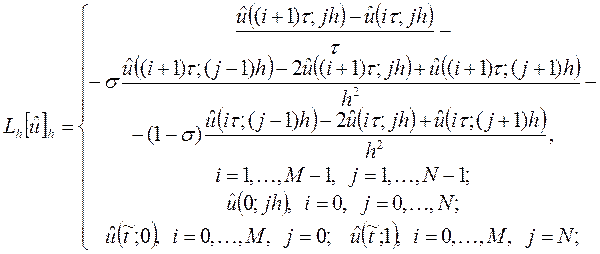
то полагая  ,
,  ,
, 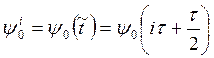 ,
, 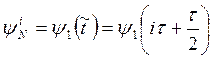 , имеем при
, имеем при 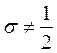
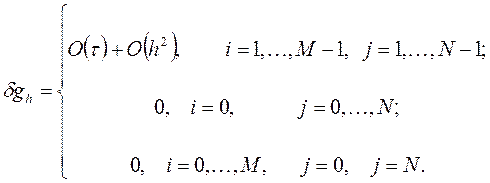
и при 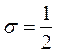
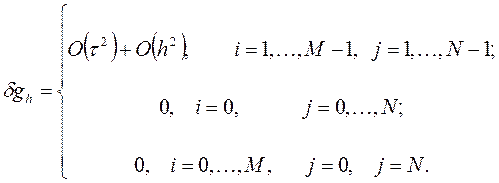
Отсюда, используя промежуточный слой 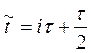 и соответствующую аппроксимацию входных данных задачи (1)-(2):
и соответствующую аппроксимацию входных данных задачи (1)-(2):  ,
,  ,
, 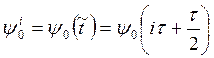 ,
, 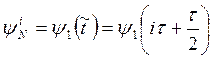 получаем, что разностная схема с весами обладает свойством аппроксимации и
получаем, что разностная схема с весами обладает свойством аппроксимации и
1)  , при
, при  ,
, 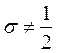 ,
,
2) 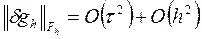 , при
, при 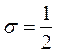 .
.
Аналогично проверяем, что явная и целиком неявная разностные схемы обладают свойством аппроксимации и  .
.
Для явной разностной схемы
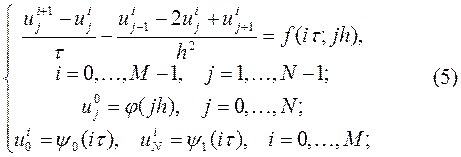
мы полагаем  ,
,  ,
, 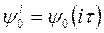 ,
, 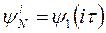 и проверяем аппроксимацию на слое
и проверяем аппроксимацию на слое 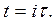
Для целиком неявной разностной схемы
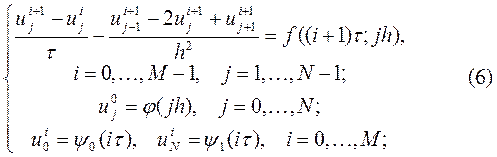
мы полагаем 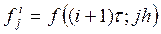 ,
,  ,
, 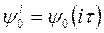 ,
, 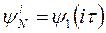 и проверяем аппроксимацию на слое
и проверяем аппроксимацию на слое 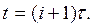
Разностная схема (4) называется устойчивой, если для достаточно малых шагов сетки 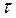 и
и 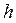 выполнены условия:
выполнены условия:
1) Для любой сеточной функции 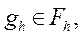 уравнение
уравнение 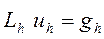 имеет единственное решение
имеет единственное решение 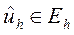 (существует обратный оператор
(существует обратный оператор 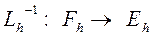 ).
).
2) Существует константа 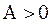 , независящая от
, независящая от 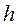 (
(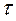 и
и 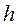 ), такая, что для решения
), такая, что для решения 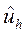 уравнения
уравнения 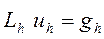 имеет место неравенство
имеет место неравенство
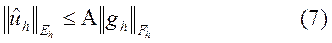
(норма обратного оператора равномерно по 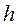 ограничена константой
ограничена константой 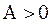 :
: 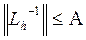 ).
).
Замечание. Условие 2) определения устойчивости разностной схемы принято называть условием устойчивости разностной схемы.
Имеет место
Предложение. Если решение 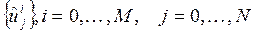 разностной схемы (4) для любого
разностной схемы (4) для любого 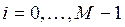 удовлетворяет условию
удовлетворяет условию
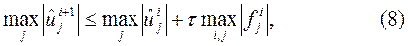
то схема (4) устойчивая.
Неравенство (6) называется принципом максимума.
Действительно, рассмотрим две разностные схемы
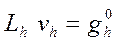 и
и 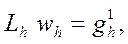
где сеточные функции 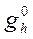 и
и 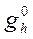 определены выражениями:
определены выражениями:
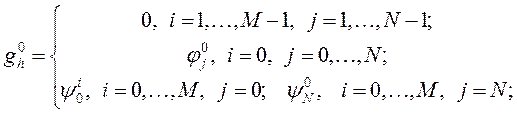
(однородное уравнение, неоднородные начальное и краевые условия) и
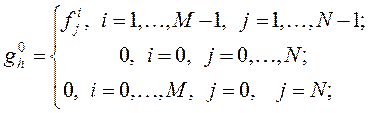
(неоднородное уравнение, однородные начальное и краевые условия).
Очевидно, если существуют решения первой и второй задач 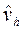 и
и 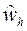 , то существует и решение
, то существует и решение 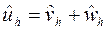 разностной схемы (4).
разностной схемы (4).
Применим принцип максимума (6) к решению 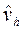 первой задачи:
первой задачи:
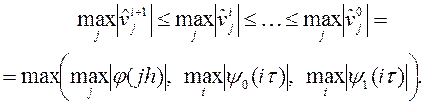
Применим принцип максимума (6) к решению 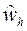 второй задачи:
второй задачи:
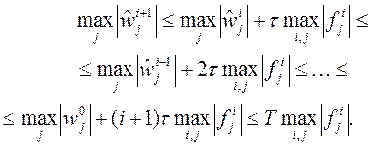
Таким образом, для решения 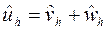 разностной схемы (4) справедливо неравенство
разностной схемы (4) справедливо неравенство
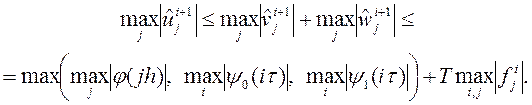
Отсюда получаем, что
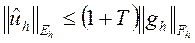 ,
,
условие устойчивости (7) выполнено с константой 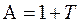 .
.
Предложение доказано.
Ограничимся исследованием устойчивости разностной схемы (4) в двух крайних случаях: целиком неявной схемы 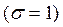 и явной схемы
и явной схемы 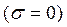 .
.
Устойчивость целиком неявной схемы 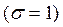 .
.
Обозначим 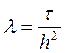 . Получим из (6) для каждого
. Получим из (6) для каждого 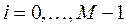
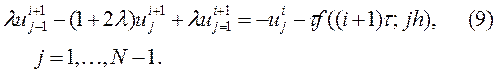
Система (9) однозначно разрешима (см. условие устойчивости метода прогонки решения системы линейных уравнений с трехдиагональной матрицей).
Пусть 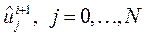 - решение (9) и
- решение (9) и 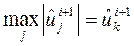 , где
, где 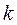 наименьший из всех индексов, для которых
наименьший из всех индексов, для которых 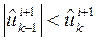 . Если
. Если 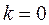 или
или 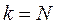 , то неравенство (8) выполнено. Пусть
, то неравенство (8) выполнено. Пусть 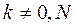 .
.
Уравнение системы (9) при 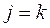 запишем в виде
запишем в виде
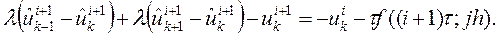
Так как сумма скобок в левой части равенства строго меньше нуля, имеем
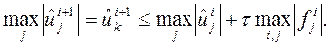
Следовательно, для целиком неявной разностной схемы имеет место неравенство (8). Это означает, что целиком неявная разностная схема устойчива при любом соотношении шагов 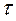 и
и 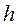 .
.
Устойчивость явной схемы 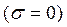
Обозначив 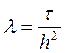 , из (5) для каждого
, из (5) для каждого 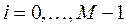 решение
решение 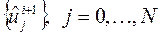 разностной схемы находится по формуле:
разностной схемы находится по формуле:
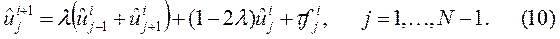
Очевидно, если 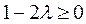 , то
, то
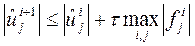
и неравенство (8) выполнено. Следовательно, явная разностная схема устойчива при условии 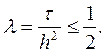
Установим, что при 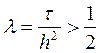 явная разностная схема является неустойчивой. Для этого достаточно показать, что, однажды возникнув, ошибка в решении будет при дальнейших вычислениях неограниченно возрастать.
явная разностная схема является неустойчивой. Для этого достаточно показать, что, однажды возникнув, ошибка в решении будет при дальнейших вычислениях неограниченно возрастать.
Рассмотрим однородную задачу 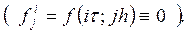 При этом схема примет вид
При этом схема примет вид
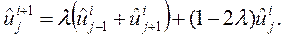
Пусть на 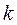 -ом слое возникла ошибки
-ом слое возникла ошибки 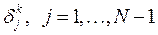 . Тогда для вычисления ошибки на следующем слое получим формулу:
. Тогда для вычисления ошибки на следующем слое получим формулу:
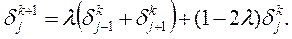
Предположим, что 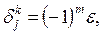
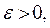 где
где 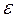 - некоторое достаточно малое число. Тогда
- некоторое достаточно малое число. Тогда
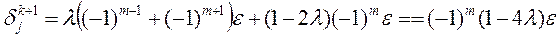
или
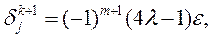
так как 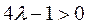 при
при 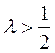 .
.
Следовательно, на слое 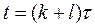 получим:
получим:
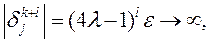 при
при 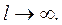
Замечание. При значительном уменьшении шага 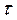 (при фиксированном
(при фиксированном 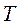 ) растет число шагов и, следовательно, растет суммарная ошибка вычислений.
) растет число шагов и, следовательно, растет суммарная ошибка вычислений.
Окончательно получаем, что явная разностная схема устойчива при 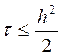 и неустойчива при
и неустойчива при 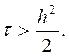
Замечание. Разностная схема (3) с весами устойчива:
1) при любом соотношении шагов, если 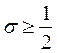 ;
;
2) при 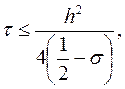 если
если 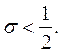
Имеет место
Теорема Филиппова. Если разностная схема (4) (то же (3)) аппроксимирует исходную дифференциальную задачу (1)-(2) на ее решении 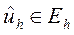 и устойчива, то она сходящаяся:
и устойчива, то она сходящаяся:
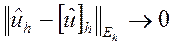 при
при 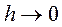
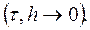
Действительно, имеем
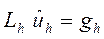 и
и 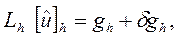
здесь 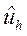 - решение разностной схемы (3) (или что тоже (4)),
- решение разностной схемы (3) (или что тоже (4)), 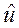 - точное решение исходной дифференциальной задачи (1) – (2).
- точное решение исходной дифференциальной задачи (1) – (2).
Отсюда получаем
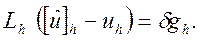
Пусть разностная схема аппроксимирует исходную задачу с порядком 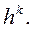 Тогда из условий аппроксимации и устойчивости немедленно следует, что
Тогда из условий аппроксимации и устойчивости немедленно следует, что
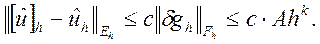
Следовательно, разностная схема является сходящейся с порядком 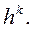
Окончательно получаем:
Разностная схема (3) с весами сходящаяся:
1) при любом соотношении шагов с порядком 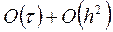 , если
, если 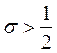 ;
;
2) при любом соотношении шагов с порядком  , если
, если 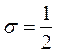 ;
;
3) при 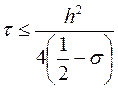 с порядком
с порядком 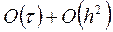 , если
, если